最適制御理論による線形システムの運動制御ー脳の設計図を求めて(2)ー
1. 脳の内部モデルとしての状態空間モデル
身体をうまく操るために、脳は身体の力学モデルを持つ必要があります。この脳の内部にあると思われる身体のモデルを「内部モデル」と呼びます。運動に関する限り、この内部モデルこそが脳の設計図に他なりません。
状態空間モデルは、脳の内部モデルを記述する数学的枠組みとして最も有力と考えられています。状態空間モデルは、制御工学の分野で発達してきた数学的枠組みで、一連の状態変数の一階連立微分(もしくは差分)方程式で物理システムを表現します。様々な状態空間モデルの中で、「線形」という特別な性質を持つ状態空間モデルが特に重要です(線形の意味については後述します)。線形な状態空間モデルにおいては、二点間を結ぶ到達問題において、評価関数を最小(大)化する軌道が、最適制御解法と呼ばれる手続きにより自動的に生成されるからです。
表1 本稿での表記法
| 記号 | 説明 | 備考 |
| \(a\) | スカラー | イタリック |
| \({\bf a}\) | ベクトル | 小文字ボールド |
| \({\bf A}\) | 行列 | 大文字ボールド |
| \({\bf A}^{\rm T}\) | 行列\({\bf A}\)の転置行列 | |
| \({\bf A}^{\rm -1}\) | 行列\(\bf{A}\)の逆行列 | |
| \(A_{ij}\) |
行列\(\bf{A}\)の\(i\)行\(j\)列要素 |
イタリック |
| \(\dot{a}\) | \(a\)の時間微分 |
本稿(第二章)では、2-5節で状態空間モデルと到達問題を数学的に定義し、6節で、これを線形な質点系の到達問題に適用して最適制御解法を説明します。7節ではまとめと今後の展開の概略を説明します。
線形な状態空間モデルそのままでは、多くの物理系に適用できません。しかし、第一章で述べたように、「局所線形化」という手法を用いると、ほとんどの力学系が線形な状態空間モデルに還元することができます。そして、それに線形最適制御解法を繰り返し適用することで、厳密な最適制御解に至るのです。局所線形化と線形最適制御解法の繰り返し適用に関しては、第三章で説明します。
本稿では、大学で習う解析学と線形代数学を使い、式を使って議論を進めます。見かけのわかりやすさを求めて式を使わず、返って回りくどい説明をする愚を犯しません。理論体系の正確な表現には式による提示は避けて通れないからです。
また、Table 1に本稿で用いる表記をまとめました。まず、スカラーは小文字のイタリックで表します。次に、ベクトルは小文字ボールド、行列は大文字のボールドで表します。行列の転置行列は右肩にロマンでTを、逆行列は-1付けて表すことにします。行列の各要素は、大文字のイタリックで表し、行と列の番号を右下に付加します。ある量の時間微分はその文字の上に点をつけて表します。
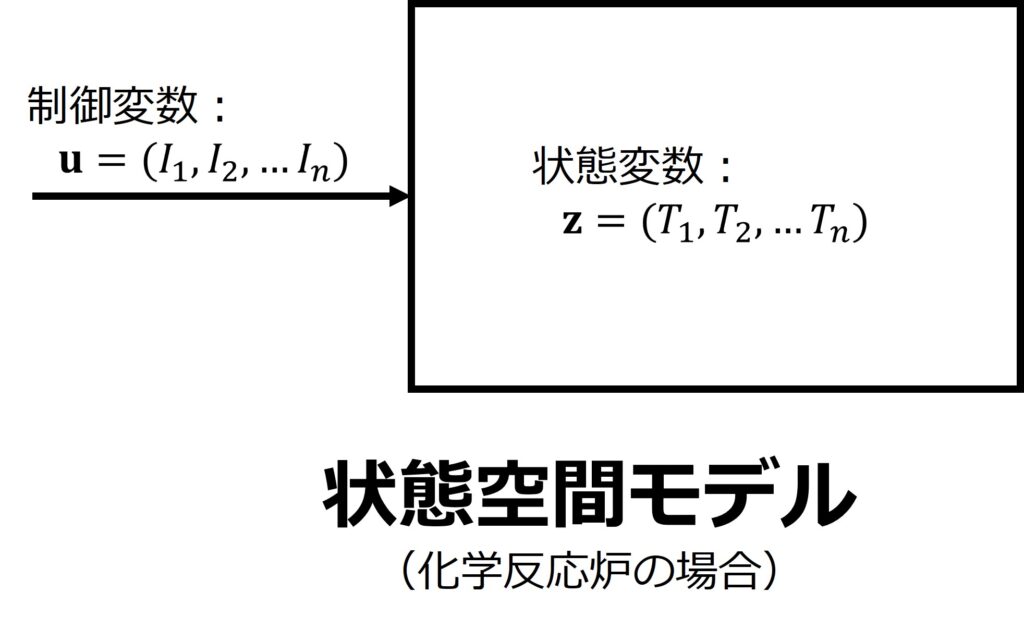
Figure 1 状態空間モデルの模式図。状態空間モデルはシステムの状態を表す状態変数ベクトル\(\bf{z}\)と、それを制御するための制御変数\(\bf{u}\)で記述されます。化学反応炉の場合、前者は炉内各所の温度の並び、後者は炉内に設置したヒーターに送る電流の並びになるかも知れません。
2. 状態空間モデル
連続時間システムの場合、系の発展を記述する状態(運動)方程式は、 \begin{equation} \dot{\bf z} ̇(t)={\bf f}({\bf z}(t),{\bf u}(t),t) \tag{1} \label{eq1} \end{equation} と一般に表されます(大塚2011)。ここで\({\bf z}(t)∈\Re^n\)は状態変数ベクトル、\({\bf u}(t)∈\Re^m\)は制御変数ベクトルです。状態変数はシステムの状態を表現しています。対象となるシステムが化学反応を進める反応炉であったとしましょう。その反応炉の状態を表す最も重要な変数は、炉内の温度かも知れません。この場合、その温度が状態変数となります。それが複数ある場合、例えば、反応炉の複数の点の温度で炉の状態を表す場合は、それらを並べたベクトル、つまり状態変数ベクトルとして一括して扱うのが便利です(Figure 1)。 一方、制御変数は、システムの制御を行うためにシステム外から与えられる変数です。化学反応炉の例では、炉を加熱するヒーターに流す電流が制御変数となるかも知れません。制御変数が複数ある場合、例えば反応炉にヒーターが複数設置されている場合などでは、制御変数も複数になります。それらを並べて制御変数ベクトルとして一括して取り扱うのが便利です。
本稿で取り扱う運動システムの場合、システム内の各部分の位置や方向、およびその1階時間微分(速度や角速度)、2階時間微分(加速度や角加速度)が状態変数になります(Figure 2)。一方、それを動かす能動装置(モーターや筋肉)の出力(力やトルク)、もしくはそれらの時間微分が制御変数になります。
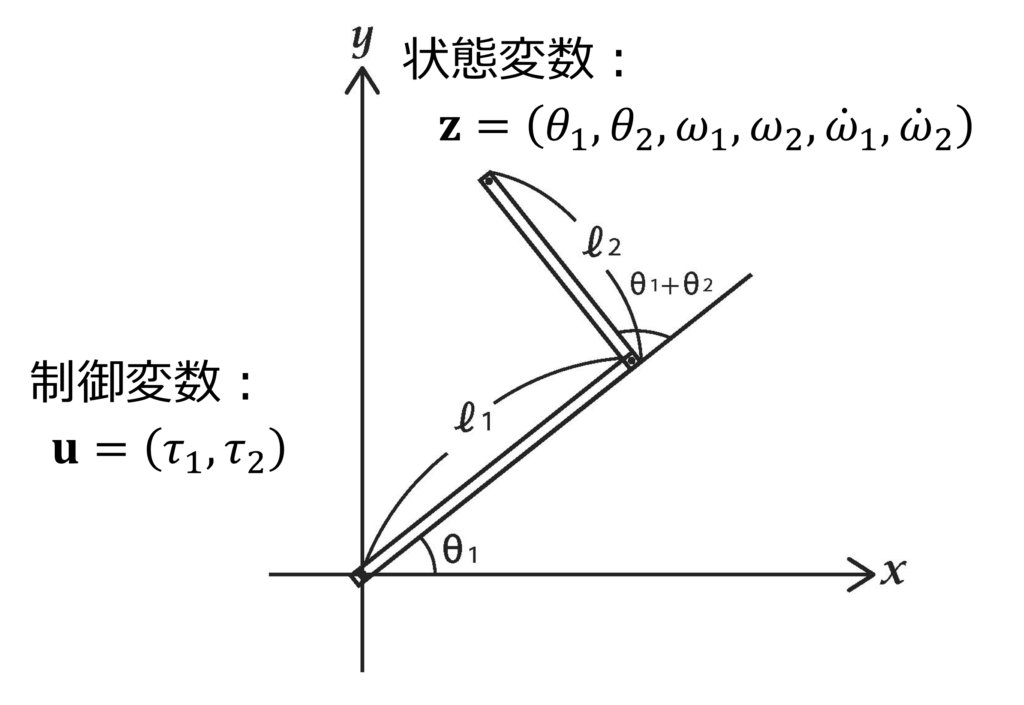
Figure 2. 二関節腕の場合、二つの関節角とその時間微分の並び\(z=(θ_1, θ_2, ω_1, ω_2, \dot{ω}_1, \dot{ω}_2 )\)が状態変数ベクトル、関節に働くトルクの列\(u=(\tau_1, \tau_2 )\)が制御変数ベクトルとなる。
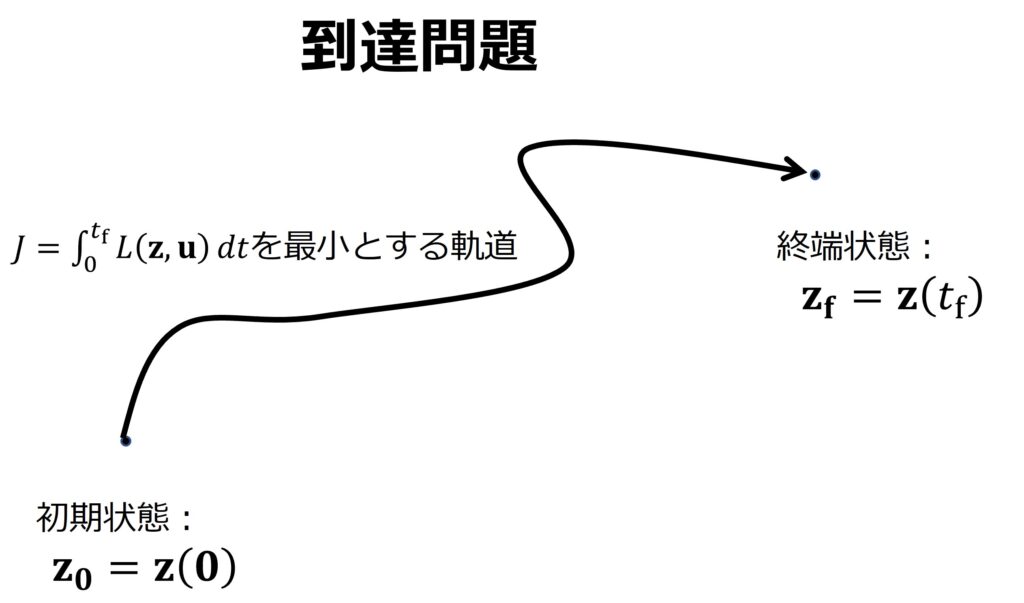
Figure 3到達問題の設定
一般には、状態変数や制御変数の一部の値が全く測定できなかったり、測定精度が悪かったりする場合もあり得ます。その場合は、どの変数がどれだけの精度で測定できるのかを表す観測方程式を定義する必要があります。これはこれで状態空間モデルの重要な機能なのですが、本稿では、観測の問題には立ち入りません。すべての状態変数と制御変数は十分な精度で分かっているとします。
3.到達問題
到達問題においては、まず、初期時刻\(t=0\)、終端時刻\(t=t_{\rm f}\)、初期状態\({\bf z}={\bf z}_0\)、終端状態\({\bf z}={\bf z}_{\rm f}\)が与えられています(Figure 3)。そこで、状態方程式のみが拘束条件である最小化問題を解いて、初期状態から終端状態に至る状態ベクトルと制御変数ベクトルの時間プロファイルを得る問題です。
最小化すべき評価関数は、
\begin{equation} J=\int_0^{t_{\rm f}}L({\bf z}(t),{\bf u}(t),t)dt \tag{2} \end{equation}
で与えられているとします。ここで、ラグランジュの未定乗数法を用いると、状態方程式(式\ref{eq1})を満たす拘束条件の下で停留条件を求める汎関数\(\bar{J}\)は、
\begin{equation} \bar{J}=\int_0^{t_{\rm f}}\left\{ L({\bf z}(t),{\bf u}(t),t)+{\bf λ}^{\rm T} ({\bf f}-\dot{\bf z})\right\} dt \tag{3} \end{equation} と与えられます。ここで、\({\bf λ}∈\Re^n\)はラグランジュの未定乗数です。ハミルトン関数を
\begin{equation} H({\bf z},{\bf u},{\bf λ},t)=L({\bf z},{\bf u},t)+{\bf λ}^{\rm T} f({\bf z},{\bf u},t) \tag{4} \end{equation}
と定義すると、
\begin{equation} \bar{J}=φ({\bf z}_{t_{\rm f}})+\int_0^{t_{\rm f}}(H({\bf z},{\bf u},{\bf λ},t)-{\bf λ}^{\rm T}\dot{z})dt \tag{5} \end{equation}
と変形できます。\(\bar{J}\) の第一変分\(δ\bar{J}\) は、
\begin{eqnarray} δ\bar{J}&=&\frac{∂φ({\bf z}(t_{\rm f}))}{∂{\bf z}} δ{\bf z}(t_{\rm f})+\int_0^{t_{\rm f}}\left(\frac{∂H}{∂{\bf z}} δz+\frac{∂H}{∂{\bf u}} δ{\bf u}-{\bf λ}^{\rm T} δ\dot{z}\right)dt\\&=&-[{\bf λ}^{{\rm T}} δ{\bf z}]_0^{t_{\rm f}}+\int_0^{t_{\rm f}}\left(\frac{∂H}{∂{\bf z}} δ{\bf z}+\frac{∂H}{∂{\bf u}} δ{\bf u}+{\bf λ}^{\rm T} δ{\bf z}\right)dt\\&=&\int_0^{t_{\rm f}}\left\{\left(\frac{∂H}{∂{\bf z}}+{\bf λ}^{\rm T} \right)δ{\bf z}+\frac{∂H}{∂{\bf u}}δ{\bf u}\right\}dt \tag{6} \end{eqnarray}
となります。ここで、部分積分を行い(第1段から第2段)、\(δ{\bf z}(0)=δ{\bf z}(t_{\rm f})={\bf 0}\)を使いました(第2段から第3段)。任意の\(δ{\bf z}\)、\(δ{\bf u}\)に対して\(δJ=0\)であるためには、すべての時刻において、以下に与えられるオイラー・ラグランジュ方程式を満たさなければなりません。
\begin{equation} \frac{∂H}{∂{\bf z}}+{\bf λ}^{\rm T}={\bf 0} \tag{7} \end{equation} \begin{equation} \frac{∂H}{∂{\bf u}}={\bf 0} \tag{8} \end{equation}
4.線形システム
状態方程式が
\begin{equation} \dot{\bf z}={\bf Az}+{\bf Bu} \tag{9} \label{eq9} \end{equation}
の形で書け、行列\({\bf A}∈\Re^{n\times n}\)と\({\bf B}∈\Re^{n\times m}\)が\({\bf z}\)にも\({\bf u}\)にも\(t\)にもよらない定数である場合、その系は線形であるといいます。また、ラグランジュ関数\(L({\bf z}(t),{\bf u}(t),t)\)が\({\bf z}\)と\({\bf u}\)の二次形式で表されるとします。つまり、
\begin{equation} L({\bf z}(t),{\bf u}(t),t)=\frac{1}{2}{\bf z}(t)^{\rm T} {\bf Qz}(t)+\frac{1}{2}{\bf u(t)}^{\rm T} {\bf Ru}(t) \tag{10} \label{eq10} \end{equation}
と置きます(\({\bf R}∈\Re^{n\times n}\)と\({\bf Q}∈\Re^{m\times m}\))。本稿では、\({\bf Q}\)と\({\bf R}\)が対称の場合を考えます。つまり\({\rm Q}={\rm Q}^{\rm T}\)、\({\bf R}={\bf R}^{\rm T}\)が、成り立つとします。オイラー・ラグランジュ方程式は、
\begin{equation} \dot{\bf λ}=-{\bf Qz}(t)-{\bf A}^{\rm T}{\bf λ} \tag{11} \end{equation}
\begin{equation} {\bf R}^{\rm T} {\bf u}(t)+{\bf B}^{\rm T} {\bf λ}={\bf 0} \tag{12} \end{equation}
となります。状態空間モデルを定義する4つの行列\({\bf A}\)、\({\bf B}\)、\({\bf Q}\)、\({\bf R}\)の要素がすべて、\({\bf z}\)にも\({\bf u}\)にもtにもよらない定数である場合(線形システム)、初期状態\({\bf z}(0)={\bf z}_0\)、終端状態\({\bf z}(t_{\rm f})={\bf z}_{\rm f}\)を満たす状態変数\({\bf z}(t)\)とそれを生み出す制御変数\({\bf u}(t)\)は、\([0,t_{\rm f} ]\)の時間区間を多数の微小区間に分割し、それぞれの区間おいて評価関数を最小化するダイナミックプログラミング手法で求めることができます。 具体的には、以下の計算手順を実行します(大塚敏之b 2011)。
手順1)以下の4つの微分方程式(式\ref{eq13}、\ref{eq14}、\ref{eq15}、\ref{eq16})を、\({\bf S}(t_{\rm f})={\bf 0}\)、 \({\bf U}(t_{\rm f})={\bf I}_n\)、\({\bf V}(t_{\rm f})={\bf I}_n\)、\({\bf W}(t_{\rm f})={\bf 0}\)の終端条件から、時間のマイナス方向に積分して、\(t=[0,t_{\rm f}]\)の区間において4つの行列\({\bf S}\)、\({\bf U}\)、\({\bf V}\)、\({\bf W}\)を求めます。
\begin{equation} \dot{\bf S}=-{\bf A}^{\rm T} {\bf S}-{\bf SA}+{\bf SBR}^{-1}{\bf B}^{\rm T} {\bf S}-{\bf Q} \tag{13} \label{eq13} \end{equation}
\begin{equation} \dot{\bf U}=-{\bf A}^{\rm T} {\bf U}+{\bf SBR}^{-1}{\bf B}^{\rm T}{\bf U} \tag{14} \label{eq14} \end{equation}
\begin{equation} \dot{\bf V}=-{\bf VA}+{\bf VBR}^{-1}{\bf B}^{\rm T}{\bf S} \tag{15} \label{eq15} \end{equation}
\begin{equation} \dot{\bf W} ={\bf VBR}^{-1}{\bf B}^{\rm T}{\bf U} \tag{16} \label{eq16} \end{equation}
ここで、\({\bf S}\)と\({\bf W}\)は対称行列、\({\bf U}\)と\({\bf V}\)は相互に転置の関係にあるので、状態変数の数を\(n\)としたとき、4個の\(n×n\)行列の\(4n^2\)個の要素のうち、独立な要素は\(2(n(n+1)/2)+n^2=2n^2+n\)個です。上記の例で挙げた一次元バネ質点系(\(n=3\))では、独立な要素の数は21個になります。
手順2)以下の式(式\ref{eq17})で\({\bf ν}\)を求めます。 \begin{equation} {\bf ν}=-{\bf W}(0)^{-1} ({\bf V}(0){\bf z}_0-{\bf z}_{\rm f} ) \tag{17} \label{eq17} \end{equation}
手順3)以下の式(式\ref{eq18}、\ref{eq19})で区間\(t=[0,t_{\rm f}]\)の\({\bf u}(t)\)および新しい\({\bf z}(t)\)を求めます。
\begin{equation} {\bf z}=-{\bf V}^{-1} ({\bf Wν}-{\bf z}_{\rm f} ) \tag{18} \label{eq18} \end{equation}
\begin{equation} {\bf u}=-{\bf R}^{-1} {\bf B}^{\rm T} ({\bf Sz}+{\bf Uν}) \tag{19} \label{eq19} \end{equation} ここで
注意しておきたいのは、初期状態と終端状態と評価関数を与えるだけで、このモデルは制御変数\({\bf u}(t)\)と\({\bf z}(t)\)の両方を出力するという意味で、順モデルと逆モデル両方の機能を備えていることです。
練習問題2-1
式\ref{eq9}と\ref{eq10}で定義される線形状態モデルの躍度最小解が手順1-3で得られることを示しなさい。また、式\ref{eq18}で得られた時間プロファイルが初期状態と終端状態を満たすことを示しなさい。
5. 躍度最小モデル
ここでいわゆる躍度最小モデル(Flash and Hogan 1985)を採用します。つまり、加速度\({\bf a}\)の時間微分(躍度:jerk)ベクトルを\({\bf g}∈\Re ^n\)と表すと、\(\frac{1}{2}{\bf g}^2\)の時間積分を評価関数とし、これを最小化するわけです。言い換えると、ラグランジュ関数\(L\)を
\begin{equation} L=\frac{1}{2} {\bf g}^2 \tag{20} \end{equation}
とします。つまり、式10において、
\begin{equation} {\bf Q}={\bf 0}, \quad{\bf R}={\bf I}_m \tag{21} \end{equation}
としたことに対応します。ここで、\({\bf I}_m\)は\(m\)行\(m\)列の単位行列です。 躍度最小モデルは、到達問題の釣り鐘型速度形状を再現し、さらにいわゆる経由点問題(複数回の連続した到達問題)において、心理物理実験で得られた結果とよく一致する結果を与えます(Flash and Hogan 1985; Todorov and Jordan 1998; Viviani and Flash 1995)。
練習問題2-2
\({\bf Q}^{\rm T}={\bf Q}\)と\({\bf R}^{\rm T}={\bf R}\)が成り立つとき、\({\bf S}={\bf S}^{\rm T}\)、\({\bf U}={\bf V}^{\rm T}\)、\({\bf W}={\bf W}^{\rm T}\)であることを示しなさい。
練習問題2-3
\({\bf Q=0}\)が成り立つとき、\({\bf S=0}\)も成立することを示しなさい。
ここで、\(t=[0, t_{\bf f}]\)の全ての時間で、\({\bf S=0}\)が成立する場合を考えてみましょう。この場合は、式\ref{eq14}、\ref{eq15}、\ref{eq16}が簡略化されて、
\begin{equation} \dot{\bf U} =-{\bf A}^{\rm T} {\bf U} \tag{22}\label{eq22} \end{equation} \begin{equation} \dot{\bf V} =-{\bf VA} \tag{23}\label{eq23} \end{equation}
\begin{equation} \dot{\bf W}={\bf VBR}^{-1} {\bf B}^{\rm T} {\bf U} \tag{24}\label{eq24} \end{equation}
となります。式\ref{eq22}より
\begin{equation} d{\bf V}/dt=-{\bf VA}=-{\bf VPΛ\tilde{P}},{\bf V}(t_{\rm f})={\bf I}_n \tag{25} \end{equation}
より
\begin{equation} {\bf V}={\bf V}(t_{\rm f} ) e^{-{\bf A}(t-t_{\rm f} ) }=e^{-{\bf A}(t-t_{\rm f} ) } \tag{26}\label{eq26} \end{equation}
を得ます。同様に式\ref{eq23}から、
\begin{equation} {\bf U}=e^{-{\bf A}^{\rm T} (t-t_{\rm f})}{\bf U}(t_{\rm f})=e^{-{\bf A}^{\rm T} (t-t_{\rm f} ) } \tag{27} \end{equation} を得ます。これらを式\ref{eq24}に代入すると
\begin{equation} \dot{\bf W}=e^{-{\bf A}(t-t_{\rm f})} {\bf BR}^{-1} {\bf B}^{\rm T} e^{-{\rm A}^{\rm T} (t-t_{\rm f})} \tag{28} \end{equation}
を得ます。両辺を積分すると
\begin{eqnarray} {\bf W}(t)&=&\int_{t_{\rm f}}^t e^{-{\bf A}(t_1-t_{\rm f} ) } {\bf BR}^{-1} {\bf B}^{\rm T} e^{-{\bf A}^{\rm T} (t_1-t_{\rm f} ) } dt_1 \tag{29} \label{eq29}\end{eqnarray}
を得ます。ここで、\({\bf R}={\bf I}_{\it m} \)のとき、\({\bf W}(t)\)は、可制御性グラム行列になります
さらに、行列\({\bf A}\)が対角化可能なとき、
\begin{equation} {\bf A}={\bf PΛP^{-1}} \tag{30}\label{eq30} \end{equation}
と固有値分解します。式\ref{eq26}に式\ref{eq30}を代入すると、
\begin{equation} {\bf V}=e^{-{\bf A}(t-t_{\rm f} ) }={\bf P}e^{-{\bf Λ}(t-t_{\rm f} ) } {\bf P}^{-1} \tag{31} \end{equation}
を得ます。また、
\begin{eqnarray} {\bf A}^{\rm T}&=&\left({\bf PΛP}^{-1}\right)^{\rm T}\\ &=&{{\bf P}^{-1}}^{\rm T} {\bf Λ}^{\rm T} {\bf P}^{\rm T} \tag{32} \end{eqnarray}
より、
\begin{eqnarray} {\bf U}&=&e^{{\bf A}^{\rm T} (t-t_{\rm f} ) }\\ &=&{\bf P^{-1}}^{\rm T} e^{{\bf Λ}(t-t_{\rm f}) } {\bf P}^{\rm T} \tag{33} \end{eqnarray}
を得ます。
\begin{eqnarray} {\bf W}(t)&=&\int_{t_{\rm f}}^t e^{-{\bf A}(t_1-t_{\rm f} ) } {\bf BR}^{-1} {\bf B}^{\rm T} e^{-{\bf A}^{\rm T} (t_1-t_{\rm f})}dt_1 \\ &=&{\bf P}\left(\int_{t_{\rm f}}^{t_1}e^{-Λ(t_1-t_{\rm f} ) } {\bf P ̃BR}^{-1} {\bf B}^{\rm T} {{\bf P}^{-1}}^{\rm T} e^{-{\bf Λ}(t_1-t_{\rm f} ) } dt_1\right) {\bf P}^{\rm T} \tag{34} \end{eqnarray}
と書けます。
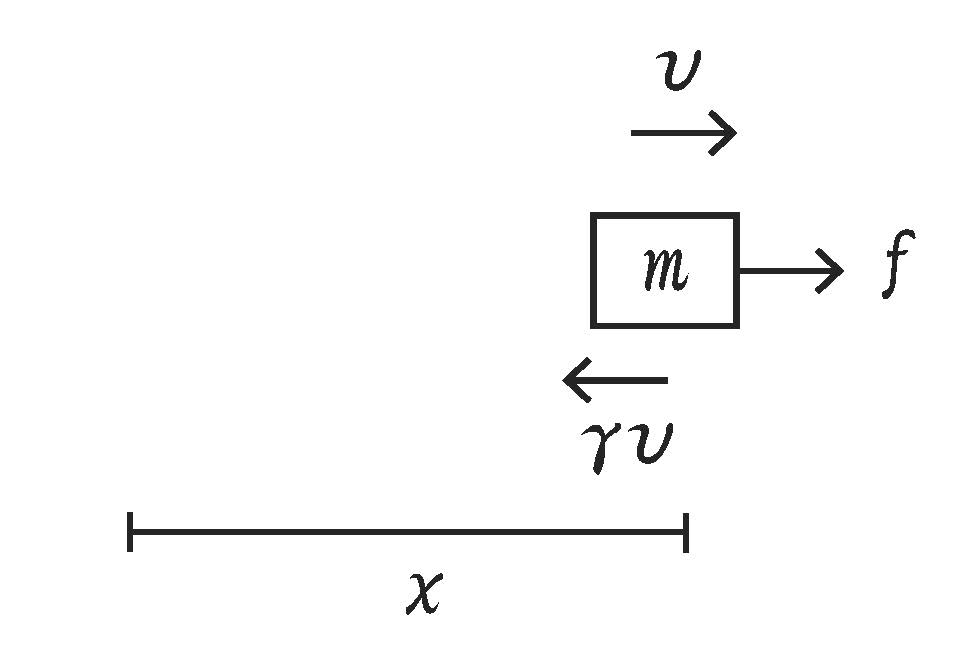
Figure 4. 一次元質点系
6. 一次元質点系
分かりやすい例として、状態空間モデルで一次元質点系を表現してみましょう(Figure 4)。質点の位置を\(x\)、速度を\(v\)、質点に働く外力\(f\)の等価加速度(\(f/m\))を\(a\)と置くと、状態方程式は以下のように書き表せます。
\begin{equation} \frac{dx}{dt}=v \tag{35} \end{equation}
\begin{equation} \frac{dv}{dt}=-γv+a \tag{36} \end{equation}
\begin{equation} \frac{da}{dt}=g \tag{37} \end{equation}
ここで、速度\(v\)に比例する抵抗力を仮定し、その係数を\(γ\)とします。また、\(g\)は躍度です。状態変数ベクトル\({\bf z}\)、制御変数ベクトル\({\bf u}\)を
\begin{equation} {\bf z}=(x\quad v\quad a)^{\rm T},\quad {\bf u}=g \tag{38} \end{equation}
と置くと \begin{equation}\frac{d{\bf z}}{dt}=\dot{\bf z}={\bf Az}+{\bf Bu} \tag{39} \label{eq39} \end{equation}
とまとめられます。ここで、行列\({\bf A}\) と\({\bf B}\)は、
\begin{equation} {\bf A}=\left( \begin{array}{cc} 0&1&0\\ 0&-γ&1\\ 0&0&0 \end{array} \right) \tag{40} \end{equation}
\begin{equation} {\bf B}=\left( \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right) \tag{41} \end{equation}
と定義されます。 では、実際に躍度最小の条件を満たす解をいくつか求めてみましょう。
6.1. 等加速度解(\(g=0\))
式\ref{eq10}の右辺\(\frac{1}{2} g^2\)を最小とする自明な解は\(t=[0, t_{\rm f}]\)のどこでも\(g=0\)を満たすものです。等価速度運動は、加速度の時間微分がいつでも0になるので、この条件を満たしています。初期状態と終端状態を等価速度運動と整合したものに設定して上記手順1-3を実行してみました(Figure 5)。\({\bf z}_0=(-1\quad 1.6\quad -0.64)^{\rm T}\)、\({\bf z}_{\rm f}=(-1\quad -1.6\quad -0.64)^{\rm T}\)、\(t_{\rm f}=5\, {\rm s}\)の場合の結果が、Figure 5に示してあります。初期、終端状態を適切に定めれば、自明な解である等価速度解が自動的に生成されます。
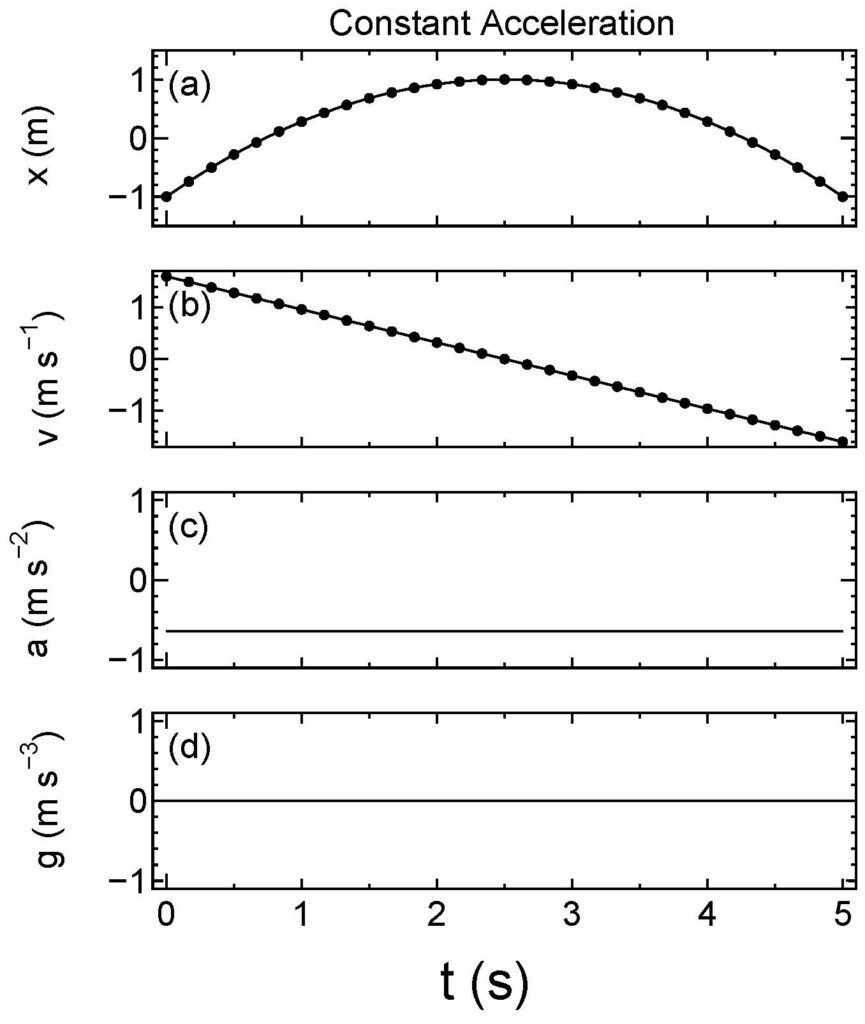
Figure 5一次元質点系の等価速度運動は、躍度最小モデルの自明な解である。\({\bf z}_0=(-1\, 1.6\, -0.64)^{\rm T}\)、\({\bf z}_{\rm f}=(-1\, -1.6\, -0.64)^{\rm T}\)の場合。
6.2. 一次元質点系の到達問題(バネ抵抗なし)
Figure 6に、一次元質点系の二点間到達運動(\({\bf z}_0=(-1\quad 0\quad 0)^{\rm T}\)、\({\bf z}_{\rm f}=(1\quad 0\quad 0)^{\rm T}\)、\(t_{\rm f}=5 \,{\rm s}\))の躍度最小解の時間プロファイルを与えます。Flash and Hogan (1985)によれば、拘束が全くない場合、一次元質点系の二点間到達運動の躍度最小解の時間プロファイルは、
\begin{equation} \frac{∂^6 x}{∂t^6}=0 \tag{42} \end{equation}
を満たします。つまり、\(x\)は\(t\)の5次式で表せることになります。各項の係数を始端と終端において\(∂^2 x/∂t^2=∂x/∂t=0\)、そして\(x(0)=x_0\)、\(x(t_{\rm f})=x_{\rm f}\)となるように定めると、
\begin{equation} x(t)=x_0+\left(x_{\rm f}-x_0)(6(t/t_{\rm f} )^5-15(t/t_{\rm f} )^4+10(t/t_{\rm f} )^3 \right) \tag{43} \label{eq43} \end{equation}
\begin{equation} v(t)=30\frac{x_{\rm f}-x_0}{t_{\rm f}} \left((t/t_{\rm f})^4-2(t/t_{\rm f})^3+(t/t_{\rm f})^2 \right) \tag{44} \label{eq44} \end{equation}
を得ます(Flash and Hogan 1985)。
練習問題2‐4
始端と終端における条件(\(∂^2 x/∂t^2 =∂x/∂t=0\)、そして\(x(0)=x_0\)、\(x(t_{\bf f} )=x_{\bf f}\))から式\ref{eq43}、\ref{eq44}を求めなさい。
式\ref{eq39}(運動方程式)という拘束条件があるFigure 6の場合、この時間プロファイル(式\ref{eq43})に完全に一致する必要はないが、求められた時間プロファイル(Figure 6aとFigure 6b)は高い精度で式\ref{eq43}と\ref{eq44}を再現しています。さらに、人間の到達運動にみられる釣り鐘型の速度プロファイルも再現しています(Figure 6b)。
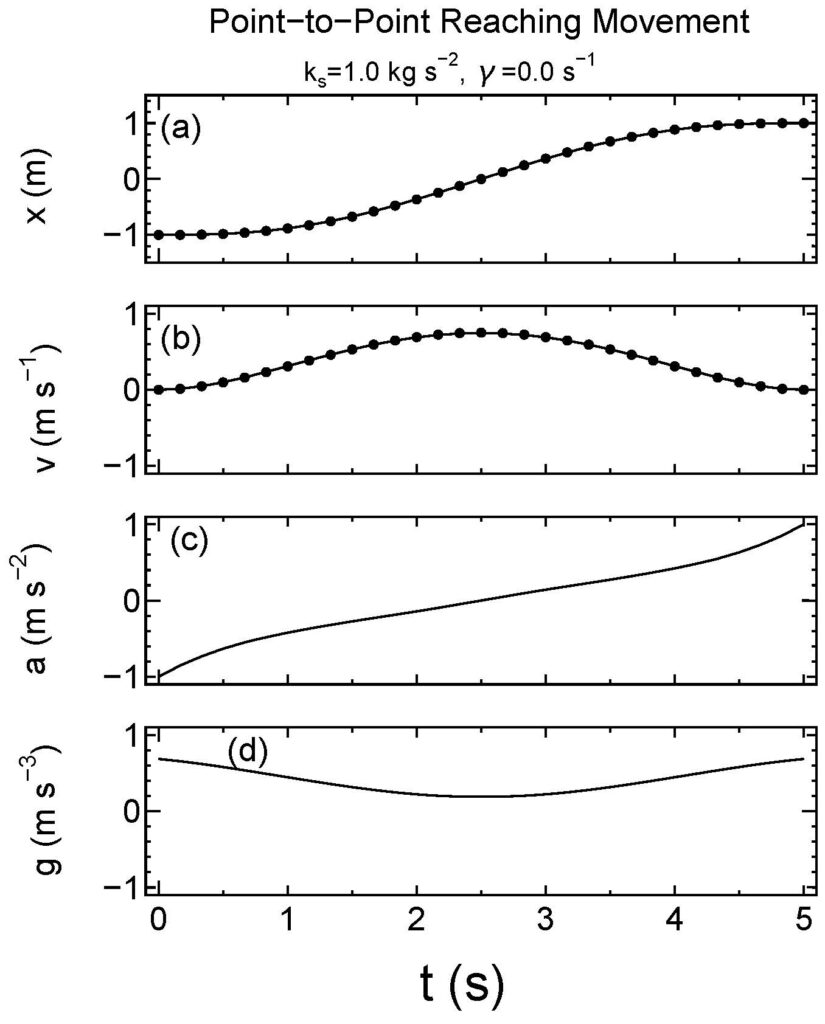
[caption id="attachment_4229" align="alignnone" width="865"]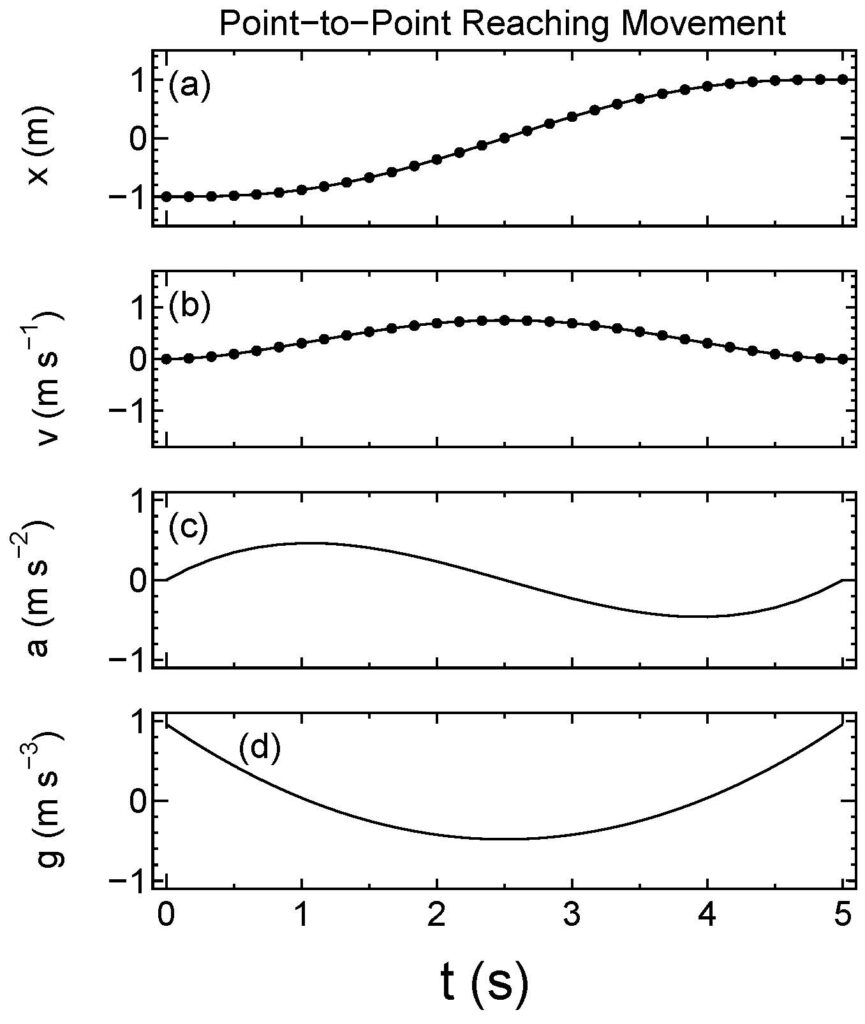 Figure 6一次元質点系の躍度最小解の状態変数の時間変化(抵抗なし:\(m=1\)、 \({\rm kg}\)、\(γ=0\,{\rm s}^{-2}\))の場合。拘束条件なしの場合の解析解(点:式\ref{eq43}、\ref{eq30})を良く再現している。
Figure 6一次元質点系の躍度最小解の状態変数の時間変化(抵抗なし:\(m=1\)、 \({\rm kg}\)、\(γ=0\,{\rm s}^{-2}\))の場合。拘束条件なしの場合の解析解(点:式\ref{eq43}、\ref{eq30})を良く再現している。
6.3. 一次元質点系の到達問題(バネあり)
次に、質点にバネを接続した一次元バネ質点系を考えます。この場合、行列\({\bf A}\)は、
\begin{equation} {\bf A}=\left( \begin{array}{cc} 0&1&0\\ -\omega^2&-γ&1\\ 0&0&0 \end{array} \right) \tag{45} \end{equation}
となります。ここで、\(\omega=\sqrt{k_{\rm s}/m}\)としました。Figure 7は、バネあり、抵抗なしの場合(\(k_{\rm s}=1\,{\rm kg\, m\, s}^{-1}\)、\(m=1\, {\rm kg}\)、\(γ=0\, {\rm s}^{-2}\))の状態変数の時間変化を式\ref{eq13}-\ref{eq19}を数値積分して求めたものを表しています。ここで、始点と終点において外力がバネの力と釣り合うようにしました。つまり、\({\bf z}_0=(-1\quad 0\quad 1)^{\rm T}\)、\({\bf z}_{\rm f}=(1\quad 0\quad -1)^{\rm T}\)です。バネの力に対抗するために躍度(一番上)と等価加速度(上から2番目)のプロファイルは変化するが、位置プロファイルは精度よく式\ref{eq42}と\ref{eq43}を再現しています。 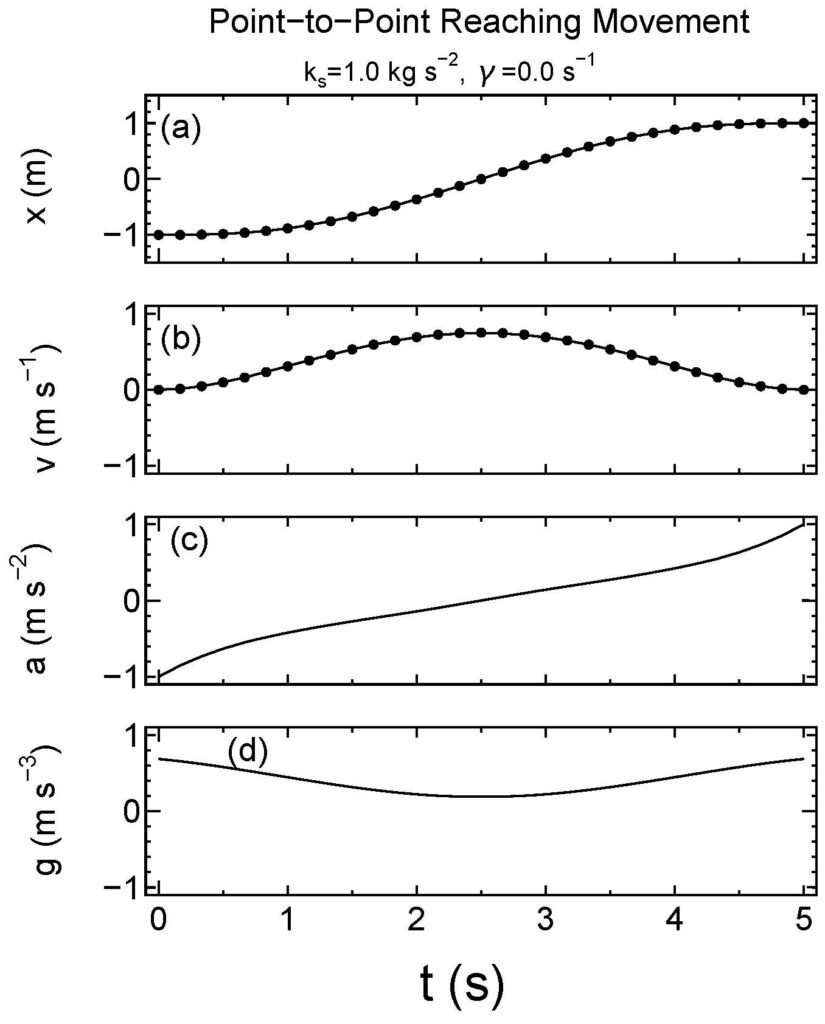
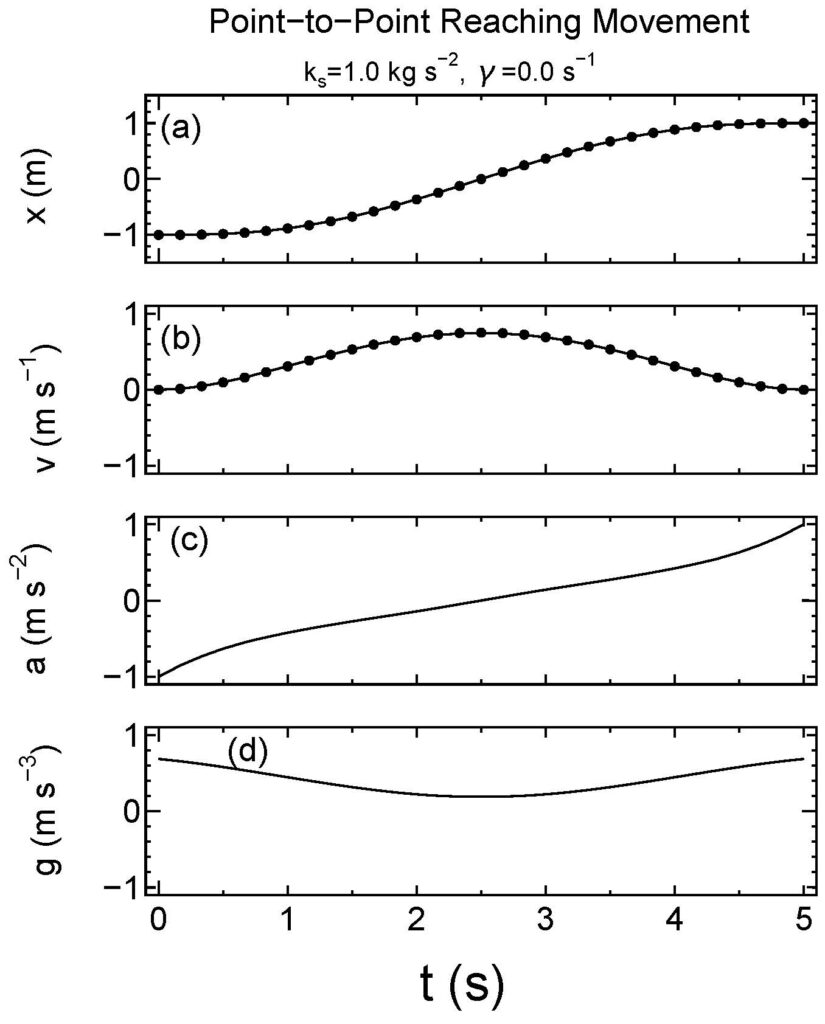
Figure 7一次元バネ質点系の躍度最小解の状態変数の時間変化。バネあり、抵抗なし(\(m=1\, {\rm kg}\),\(k_{\rm s}=1\, {\rm kg}\, {\rm s}^{-2}\)、\(γ=0\, {\rm s}^{-2}\))の場合。バネの力に対抗するために力のプロファイルは変化するが、位置プロファイルは精度よく式28、29を再現している。
練習問題2-5
式\ref{eq30}を用いて\({\bf W}(t)\)を解析的に求めなさい。
また、Figure 8に到着時間を10秒に伸ばした場合の解を表しています。この場合、固有振動(周期\(2π\)秒)の影響で、解析解からの解離がより大きくなります。
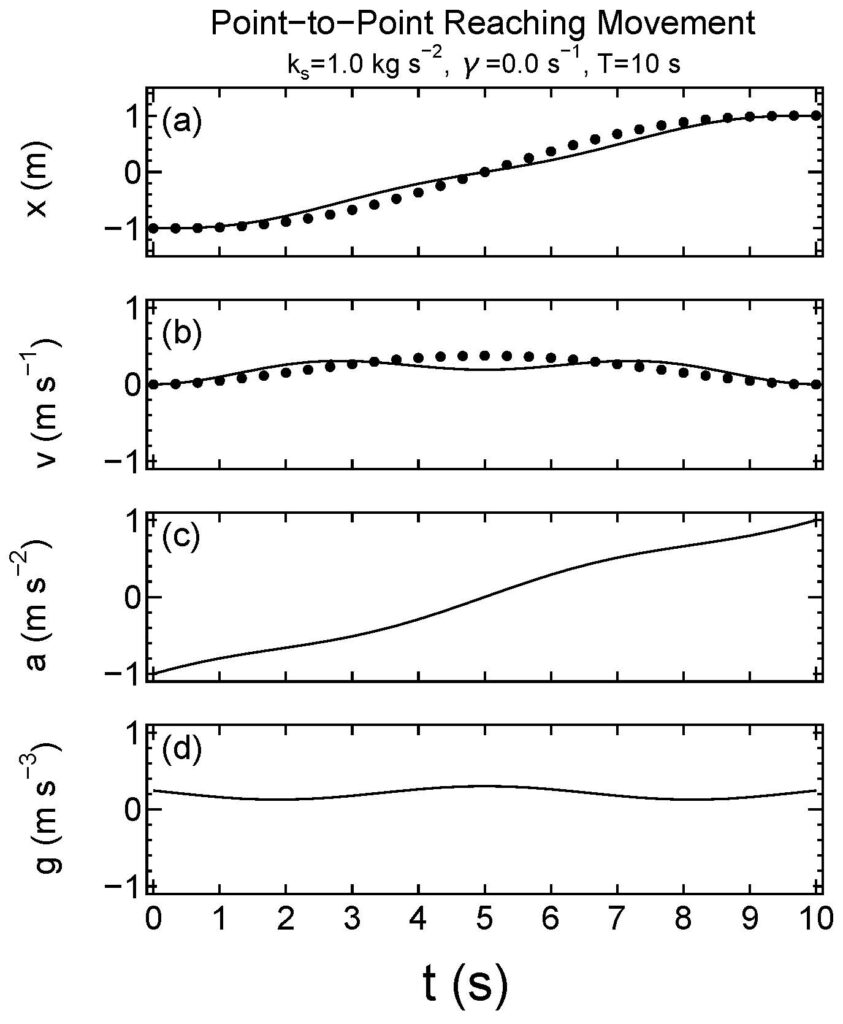
Figure 8一次元バネ質点系の躍度最小解の状態変数の時間変化。バネあり、抵抗なし(\(m=1 \,{\rm kg}\)、\(k_{\rm s}=1 \,{\rm kg\, s}^{-2}\)、\(γ=0\, {\rm s}^{-1}\))の場合。到達時間Tを10秒に伸ばすと、固有振動数の効果が表れて解析解からのずれが大きくなる
6.4. 一次元質点系の到達問題(抵抗あり)
さらに、バネはないが、抵抗がある場合(\(m=1\, {\rm kg}\)、\(k_{\rm s}=0\, {\rm kg\, s}^{-1}\)、\(γ=1\, {\rm s}^{-2}\))の結果をFigure 9に示します。同様に、抵抗に抗うために躍度のプロファイル(一番上の図)と等価加速度のプロファイル(上から2番目の図)はFigure 6から変化しますが、位置プロファイルは精度よく式27を再現しています。 このように、バネや抵抗などによる力が加わっても頑健に式27のプロファイルが維持されるように躍度が自動調節されています。ここには示しませんが、バネと抵抗の両方がある場合も同様に調節されます。
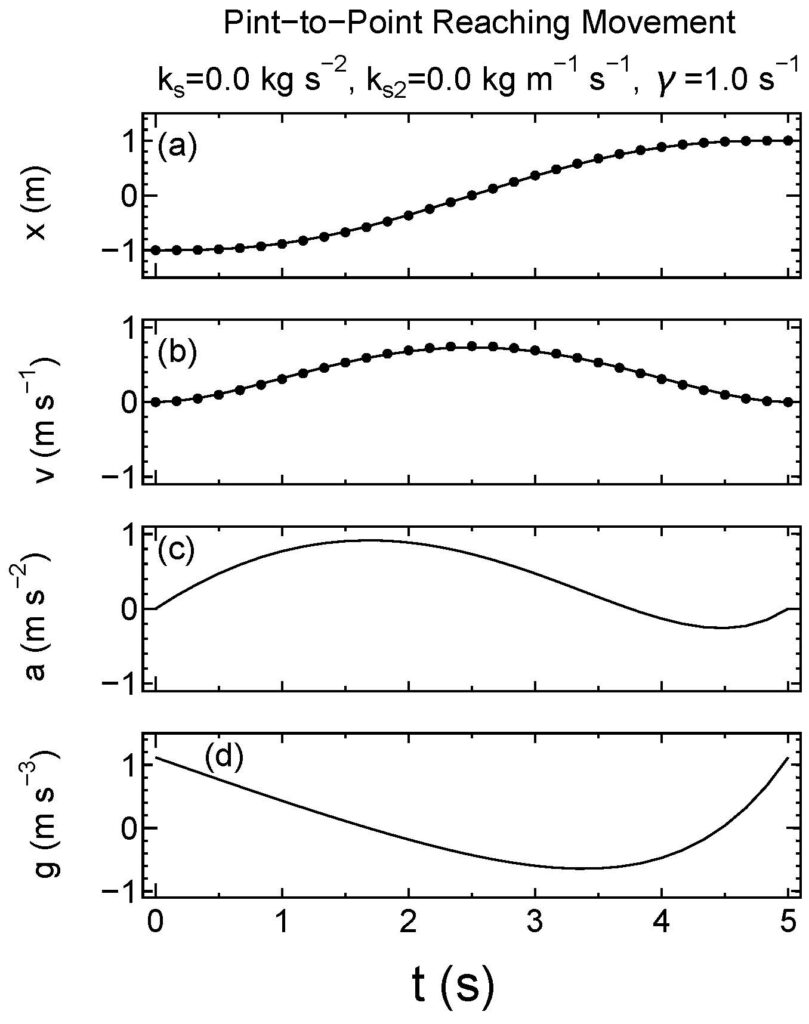
Figure 9一次元バネ質点系の躍度最小解の状態変数の時間変化。バネなし、抵抗あり(\(m=1\, {\rm kg}\)、\(k_{\rm s}=0\, {\rm kg}\, {\rm s}^{-2}\)、\(γ=1\, {\rm s}^{-2}\))の場合。抵抗力に対抗するために躍度と等価加速度のプロファイル(cとd)が変化している。
7. まとめと今後の展開
本章(第二章)では、まず状態空間モデルについて解説し、線形な状態空間モデルの場合について到達問題の最適制御解を自動的に得る手法について解説しました。そして、一次元質点系の様々な場合(等速度運動とバネ、抵抗力がある場合の質点の運動)について、この最適制御解法を適用して開始状態と終端状態を満たす軌跡とそれの実現するための制御変数の最適な時間プロファイルが実際に得られることを示しました。 これらの結果を見て私は、最適制御解法(式\ref{eq13}‐\ref{eq19})を実行する神経回路が脳の中に内部モデルとして存在していて、運動制御に使われていると考えるようになりました。その神経回路を「最適制御神経回路」と呼ぶことにします。
マーは1982年に神経科学の理論的枠組みを考える際、「計算理論」、「表現とアルゴリズム」、「実装」の3つのレベルに分けて考えることを提唱しました(Mar 1982)。運動制御に関しての脳は、計算理論レベルで最適制御理論、表現とアルゴリズムレベルで最適制御解法(式\ref{eq13}‐\ref{eq19})、そして実装レベルで、最適制御神経回路に対応していると私は考えます(Table 2)。
Table 2 Marrの計算レベルとの対応
| 計算レベル | 本稿の仮説 |
| 計算理論 | 運動制御理論 |
| 表現とアルゴリズム | 最適制御アルゴリズム(式\ref{eq13}-\ref{eq19}) |
| 実装 | 最適制御神経回路 |
本稿では、この作業仮説に沿って脳の設計図について議論してみたいと思います。 その基本構造は以下のようなものを考えています(あくまで現時点でのもので、変わるかもしれません)。
まず、続く2章(第3章と第4章)でアルゴリズムレベルの議論を続けます。第3章ではまず、非線形な状態空間モデルでも局所線形化して線形最適制御解法を繰り返し適用することで最適解が得られることを示します。そして、バネや抵抗の力が非線形成分を持つ場合や、与えられた曲線に拘束されて動く一次元質点系(状態変数が3個)の到達問題を実際に解いて、ヒトの心理物理実験の結果と比較します。
第4章では、さらに二関節腕のような二次元システム(状態変数が6個)に最適制御解法を適用してさらに様々な人の物理心理実験の結果と比較します。 第5章では、状態空間モデル定義する行列(\({\bf A}\)、\({\bf B}\)、\({\bf Q}\)、\({\bf R}\)など)を経験的に決める手法について説明します。工学の分野ではこの作業をシステム同定と呼んでいます。第4章までは、運動方程式を立て、微分や積分などを用いて求めておりました。しかし、ヒトや動物は、筋肉で体を動かしながら必要な行列の各要素を決め、実際に最適な動きを生成しているはずです。生まれたばかりの赤ん坊は、最初は無暗に手足をばたばたさせていますが、だんだん各部の運動の連携が取れるようになり、終には寝返りを打ちます。あの赤ん坊の無暗な手足の運動は、決して無駄な動きではなく、脳内モデルを構成する状態空間モデルを定義する行列を学習するために必要な動きと考えられます。
第6章では、最適制御アルゴリズムを離散化し、神経回路網(ニューラルネット)の学習に適用する手法について記述します。それは、AI構築の際に問題になっている神経回路網の学習の収束の速さを決める因子を与える数学的枠組みを提供します。 さらに第7章では、神経細胞を基本素子として、最適制御神経回路の実装に論を進めます。最適制御解法の計算は行列積ひいてはベクトル同士の内積計算が大部分を占めます。神経細胞はベクトルの内積計算を実行するに最適な構造を持っています。非常にたくさんの神経細胞が存在する脳は、多数の行列積を並列に実行する最適制御解法を実装するのに適したの計算システムと言えるでしょう。
また、計算の一部には、前節(第6章)で説明した手法で構成した神経回路網(ニューラルネット)の機能ユニットを用います。 また、余力があったらセンサー系と制御系の類似性について、7章以降で議論したいと思います。
謝辞
五十嵐潤さん、太田聡さん、奥村雅彦さんに、本稿で紹介した計算手法とその結果について議論をしてもらいました。
1) 大塚敏之a、2011、5章連続システムの最適制御、非線形最適制御入門、コロナ社、pp102-120。
2) 大塚敏之b、2011、5章練習問題3、非線形最適制御入門、コロナ社、pp206-207。
3) Flash, T. and Hogan, N. 1985, The coordination of arm movements: an experimentally confirmed mathematical model, Journal of Neuroscience, 5, 1688-1703.
4) Todorov, E. and Jordan, M.I., 1998, Smoothness maximization along a predefined path accuracy predicts the speed profiles of complex arm movements, Journal of neurophysiology, 80, 89-101.
5) Viviani, P., and Flash, T., 1995, Minimum-jerk, two thirds power law, and isochrony: converging approaches to movement planning, The journal of Experimental Psychology: Human Perception and Performances, 21, 32-53.
6) Marr, D., 1982, Vision: A Computational Investigation into the Human Representation and Processing of Visual Information, W.H. Freeman.
初出:TEN (Tsunami, Earth, and Networking) 第6巻、pp38‐46
その後の理解の進展により一部変更している。
書籍版『科学はひとつ』のご案内
戎崎俊一 著
学而図書/四六判 並製320頁/本体2,400円+税
12年にわたり執筆されてきた記事を精選し、「地震と津波防災」など全9章に再編。すべての章に著者書き下ろしの解説を加えて集成した一冊。



