練習問題2-1の解答
練習問題2-1
式2-9と2-10で定義される線形状態モデルの躍度最小解が手順1-3で得られることを示しなさい。また、式2-18で得られた時間プロファイルが初期状態と終端状態を満たすことを示しなさい。
練習2-1の解答
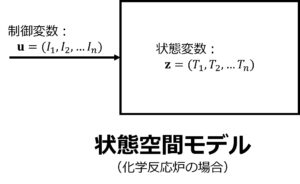
状態(運動)方程式は
\begin{equation} \dot{\bf z} = {\bf Az}+{\bf Bu} \tag{1} \label{eq1}\end{equation}
で与えられる。オイラー・ラグランジュ方程式は式2-13と2-14より、
\begin{equation} \dot{\bf λ} =-{\bf Qz}-{\bf A}^{\rm T} {\bf λ} \tag{2} \label{eq2}\end{equation} \begin{equation} {\bf R}^{\rm T} {\bf u}+{\bf B}^{\rm T} {\bf λ}={\bf 0} \tag{3} \label{eq3}\end{equation}
と与えられる。これら3つの方程式を連立して解く。未知数は\({\bf z}(t)∈\Re^{\rm n}\)、\({\bf u}(t)∈\Re^{\rm m}\)、\({\bf λ}(t)∈\Re^{\rm n}\)でその数は\(2n+m\)個である。一方、方程式の数は式\ref{eq1}が\(n\)本、式\ref{eq2}が\(n\)本、式\ref{eq3}が\(m\)本で全部で\(2n+m\)本存在する。したがって、未知数が方程式の数と一致する。
ここで、\({\bf λ}(t)\)と\({\bf z}(t_{\rm f})\)を\({\bf z(t)}\)と\({\bf ν}\)の線形結合で表す。つまり、
\begin{equation} {\bf λ}(t)={\bf S}(t){\bf z}(t)+{\bf U}(t){\bf ν}\label{eq4} \tag{4} \end{equation}
\begin{equation} {\bf z}(t_{\rm f})={\bf V}(t){\bf z}(t)+{\bf W}(t){\bf ν}={\bf z}_{\rm f} \tag{5}\label{eq5} \end{equation}
とする。ここで、
\begin{equation} {\bf S}(t_{\rm f})={\bf 0},\quad {\bf U}(t_{\rm f})={\bf I}_{n},\quad {\bf V}(t_{\rm f})={\bf I}_{n},\quad {\bf W}(t_{\rm f})={\bf 0} \tag{6} \label{eq6}\end{equation}
とする。これらを式\ref{eq4}に代入すると
\begin{equation} {\bf ν}={\bf λ}(t_{\rm f}) \tag{7} \end{equation}
を得る。
次に、式\ref{eq2}に式\ref{eq4}を代入すると
\begin{equation} \dot{\bf λ} =\dot{\left({\bf S}(t){\bf z}(t)+{\bf U}(t){\bf ν}) \right)} =-{\bf Qz}(t)-{\bf A}^{\rm T} \left({\bf S}(t){\bf z}(t)+{\bf U}(t){\bf ν}\right) \tag{8} \end{equation}
を得る。したがって、
\begin{equation} \dot{\bf S} ̇{\bf z}+{\bf S}\dot{\bf z} +\dot{\bf U} {\bf ν}=-{\bf Qz}-{\bf A}^{\rm T} ({\bf Sz}+{\bf Uν}) \tag{9}\label{eq9} \end{equation}
となる。式\ref{eq9}に式\ref{eq1}を代入する。
\begin{equation} \dot{\bf S} {\bf z}+{\bf S}({\bf Az}+{\bf Bu})+\dot{\bf U} {\bf ν}=-{\bf Qz}-{\bf A}^{\rm T} ({\bf Sz}+{\bf Uν}) \tag{10} \label{eq10}\end{equation}
一方、式\ref{eq3}より \begin{equation} {\bf Ru}+{\bf B}^{\rm T} {\bf λ}={\bf 0} \tag{11} \end{equation}
である。これを\({\bf u}\)について解いて、式\ref{eq4}を代入する。
\begin{eqnarray} {\bf u}&=&-{\bf R}^{-1} {\bf B}^{\rm T}{\bf λ}\\ &=&-{\bf R}^{-1} {\bf B}^{\rm T} ({\bf Sz}+{\bf Uν}) \tag{12} \label{eq12}\end{eqnarray}
式\ref{eq10}に式\ref{eq12}を代入すると、
\begin{equation} \dot{\bf S} {\bf z}+{\bf SAz}-{\bf SBR}^{-1} {\bf B}^{\rm T} ({\bf Sz}+{\bf Uν})+\dot{\bf U} {\bf ν}+({\bf Q}+{\bf A}^{\rm T} {\bf S}){\bf z}+{\bf A}^{\rm T} {\bf Uν}={\bf 0} \tag{13} \end{equation}
\begin{eqnarray} &&\left(\dot{\bf S} +{\bf A}^{\rm T} {\bf S}+{\bf SA-SBR}^{-1} {\bf B}^{\rm T} {\bf S}+{\bf Q}\right){\bf z}\\ &+&\left(\dot{\bf U} +{\bf A}^{\rm T} {\bf U}-{\bf SBR}^{-1} {\bf B}^{\rm T} {\bf U}\right){\bf ν}={\bf 0} \tag{14} \label{eq14}\end{eqnarray}
を得る。任意の\({\bf z}\)と\({\bf ν}\)で式\ref{eq14} が成立するために、
\begin{equation} \dot{\bf S} +{\bf A}^{\rm T} {\bf S}+{\bf SA-SBR}^{-1} {\bf B}^{\rm T} {\bf S}+{\bf Q}={\bf 0} \tag{15} \end{equation} と \begin{equation} \dot{\bf U} +{\bf A}^{\rm T} {\bf U}-{\bf SBR}^{-1} {\bf B}^{\rm T} {\bf U}={\bf 0} \tag{16} \end{equation}
が成り立つ必要がある。
一方、式\ref{eq5}の両辺を微分すると、
\begin{equation} \dot{\bf V}{\bf z}+{\bf Vz} ̇+\dot{\bf W} {\bf ν}={\bf 0} \tag{17} \label{eq17}\end{equation}
を得る。式\ref{eq17}に式\ref{eq1}を代入する。
\begin{equation} \dot{\bf V} {\bf z}+{\bf V}({\bf Az}+{\bf Bu})+\dot{\bf W} {\bf ν}={\bf 0} \tag{18} \end{equation}
さらに、式\ref{eq12}を代入する。
\begin{equation} \dot{V} {\bf z}+{\bf VAz}-{\bf VBR}^{-1} {\bf B}^{\rm T} ({\bf Sz}+{\bf Uν})+\dot{\bf W} {\bf ν}={\bf 0} \tag{19} \end{equation} \begin{equation} ({\bf V} ̇+{\bf VA}-{\bf VBR}^{-1} {\bf B}^{\rm T} {\bf S}){\bf z}+(\dot{\bf W} -{\bf VBR}^{-1} {\bf B}^{\rm T} {\bf U}){\bf ν}={\bf 0} \tag{20}\label{eq20}\end{equation}
任意の\({\bf z}\)と\({\bf ν}\)で式\ref{eq20} が成立するためには、
\begin{equation} \dot{\bf V} +{\bf VA}-{\bf VBR}^{-1} {\bf B}^{\rm T} {\bf S}={\bf 0} \tag{21} \end{equation} と \begin{equation} \dot{\bf W} -{\bf VBR}^{-1}{\bf B}^{\rm T} {\bf U}={\bf 0} \tag{22} \end{equation}
が成り立つ必要がある。
ここで、式\ref{eq5}に\(t=0\)を代入する。
\begin{equation} {\bf V}(0){\bf z}(0)+{\bf W}(0){\bf ν}={\bf z}_{\rm f} \tag{23} \end{equation}
\({\bf ν}\)について解くと
\begin{eqnarray} {\bf ν}&=& -{\bf W}(0)^{-1} \left({\bf V}(0){\bf z}(0)-{\bf z}_{\rm f} \right)\\ &=&-{\bf W}(0)^{-1} \left({\bf V}(0){\bf z}_0-{\bf z}_{\rm f} \right) \tag{24} \end{eqnarray}
を得る。 一方、式\ref{eq5}を\({\bf z}(t)\)について解く。
\begin{equation} {\bf z}(t)=-{\bf V}(t)^{-1} \left({\bf W}(t){\bf ν}-{\bf z}_{\rm f} \right) \tag{25} \end{equation}
\(t=t_{\rm f}\)を代入して、\({\rm V}(t_{\rm f}){\bf V}(t_{\rm f})^{-1}={\bf I}_{n}\)、\({\bf W}(t_{\rm f})={\bf 0}\)に注意すると、
\begin{equation} {\bf z}(t_{\rm f})=-{\bf I}_{n} ({\bf 0ν}-{\bf z}_{\rm f} )={\bf z}_{\rm f} \tag{26} \end{equation}
つまり、終端条件\({\bf z}(t_{\rm f})={\bf z}_{\rm f}\)
が成立していることが確認された。
また、\(t=0\)を代入して、式\ref{eq6}を考慮すると
\begin{eqnarray} {\bf z}(0)&=&-{\bf V}(0)^{-1} ({\bf W}(0)(-{\bf W}(0)^{-1} ({\bf V}(0){\bf z}_0-{\bf z}_{\rm f} ))-{\bf z}_{\rm f} ) \\ &=&-{\bf V}(0)^{-1} (-{\bf W}(0){\bf W}(0)^{-1} ({\bf V}(0){\bf z}_0-{\bf z}_{\rm f} )-{\bf z}_{\rm f} )\\ &=&-{\bf V}(0)^{-1} (-({\bf V}(0){\bf z}_0-{\bf z}_{\rm f} )-{\bf z}_{\rm f} ) \\ &=&-{\bf V}(0)^{-1} (-{\bf V}(0){\bf z}_0+{\bf z}_{\rm f}-{\bf z}_{\rm f} )\\ &=&{\rm z}_0 \tag{27} \end{eqnarray}
つまり、初期条件\({\bf z}(0)={\bf z}_0\)が成立していることが確認された。
書籍版『科学はひとつ』のご案内
戎崎俊一 著
学而図書/四六判 並製320頁/本体2,400円+税
12年にわたり執筆されてきた記事を精選し、「地震と津波防災」など全9章に再編。すべての章に著者書き下ろしの解説を加えて集成した一冊。