脳の設計図を求めてーはじめにー
1. はじめに
戎崎は西暦2000年ぐらいから、人間の脳を超える能力をもった人工脳を作りたいと考えていました。手塚治虫の漫画「鉄腕アトム」では2003年にアトムが製作されることになっています。そろそろアトムのような人間と理解し会える高度な人工脳ができるのではないかと考えたのです。では、どうすればいいでしょうか?

Figure 1. 鉄腕アトムの主要キャラクター。右からアトム、お茶の水博士、そしてウラン。アトムが指し示している赤いハートの物体は、善悪を見分けられる装置であるらしい。
2. 第一目標:何はともあれEflopsを実現しよう‐人間全脳実時間シミュレーションへの挑戦
まず、人間の脳の計算能力を評価してみました。人間の脳にはだいたい\(10^{11}\)個の神経細胞があると言われてます。このうち8割の神経細胞は小脳に、残りの2割が大脳に存在します。ただし、大脳の神経細胞は平均一万個の入力信号を処理しており、計算能力としては大脳の方が大きくなります。個々の神経細胞は大体1ミリ秒に一回、約1万個の別の神経細胞からの出力を受けて積和演算を行い、活性化関数を計算しています。この積和演算に必要な計算能力は \begin{equation} 2\times 0.2\times 10^{11}\times 10^4/10^{-3}=0.4\times 10^{18} {\rm flops}=0.4 {\rm Eflops} \tag{1} \end{equation} と評価できます。ここで、積和演算は掛け算と足し算の2演算と数えています。2000年ころは、世界最高速のスパコンがようやく2Tflopsの演算性能を達成していた状況でした(Figure 1)。つまり、当時の最高性能のスパコンと比較しても100万倍の性能のものすごいコンピュータを人間一人一人が持っていることに気づきました。人間の脳は約400kcal相当のブドウ糖を1日に消費すると言われています。これは、20W足らずの消費電力に相当します。計算機としての人間脳は演算性能をとってもそのエネルギー効率から見ても当時のスパコンが足元にも及ばない性能を持っていたのです。
これだけハードウエアの仕様が違うと、ソフトウエア(使い方の工夫)だけで人間の脳に匹敵するものを作るのは不可能と私は思いました。逆に言うと、Eflopsを超えるような高性能計算機が日常使いされるようになれば、現在人間が行っている多くの知的労働が計算機で代替されるようになると私は考えました。その後2005年に、カーツワイルが”The Singularity Is Near”(Kurzweil 2005.)と題した本を書き話題になりました。私と同じようなことを考える人も世界にはいるもんだなと私は思いました。その後「技術的特異点」に関してはたくさんの本が書かれて話題になっています。
そこで、まず人間の脳の実時間シミュレーションを実現する努力を始めました。電気通信大学の山﨑匡さんと沖縄科学技術大学(当時)の五十嵐潤さんは、JAMSTECの暁光を使って、2017年にネコ規模小脳のリアルタイムシミュレーションを実現しました(Yamazaki et al. 2017)。牧野淳一郎さんと私は、山﨑さんが開発したOpenCLのコードのレビューなどを実施してその高速化に協力しました。その後、五十嵐さんと山﨑さんは富岳を使った大規模な神経回路シミュレーションの実現のために、MONET (Millefeuille-like Organization NEural network) (Igarashi et al. 2019)というタイル分割と最小信号伝搬遅延時間間隔での非同期一対一通信を可能とするソフトウエアフレームワークを開発していました。神戸大学(当時)の野村昴太郎さんと牧野淳一郎さんと私はMONETのコードレビューなどを実施してその高速化に協力しました。その後彼らは着々と準備を整え (Yamaura et al. 2020)、2022年に人間の全脳の半分に相当する(450億個)規模の神経回路網のリアルタイムシミュレーションを五十嵐さん、山﨑さんの努力で実現しました (Yamazaki et al. 2021; Igarashi et al. 2022)。こうして私が設定した第一目標がほぼ達成されました。
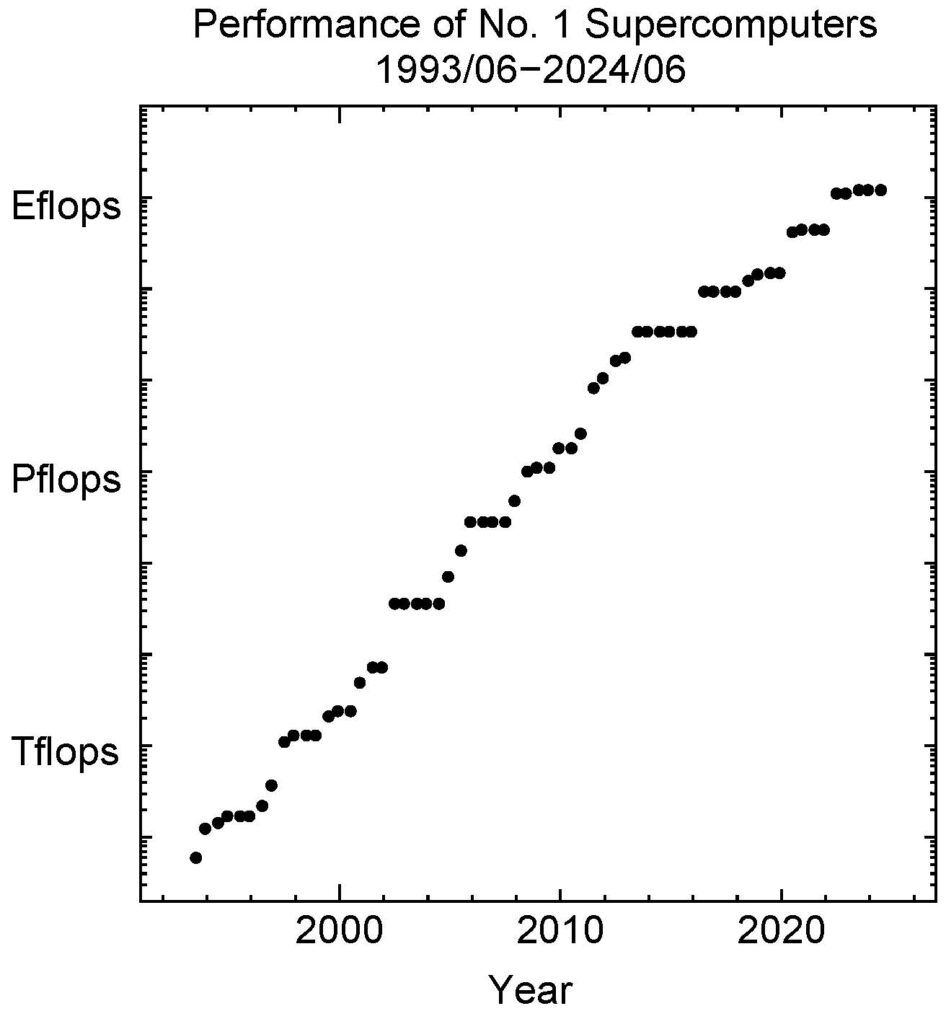
Figure 2.高性能計算機用のベンチマークLINPACK性能のリストが1993年以来6月と11月の二回まとめられてTop500として発表されてきた。2000年には約2.4 TFlopsだった。現在(2024年)は、1.2 EFlopsに到達している。https://top500.org/
3. 第二目標:読み・書き・算盤
次の目標として、何か人間らしい問題を人工脳に解かせたいと私は考えました。小学校に入って人間の子供が行うような作業は何でしょう?それは「読み・書き・算盤」だと私は思いました。もう少し具体的には、小学生用の算数、漢字ドリルをさせられないでしょうか。まず、算数ドリルはどうでしょう。ドリルの数字を読んで理解することは、最近の畳み込みニューラルネットワーク(Convolutional Neural Network)の発達で既に可能になっているし、その計算に関しては、計算機は得意です。既に人間の能力をはるかに上回っています。しかし、その結果をドリルの枠の中に書き込まなければなりません。枠を認識しその中に鉛筆で書き込むための腕の制御はなかなか大変そうな気がしました。次に、漢字ドリルはどうでしょうか?最近のAIは漢字も認識できそうです。その結果をもとに、穴埋め問題の答えを用意することは、既にできそうです。しかし、その結果を期待されるマスのなかに書き込む作業は、数字の場合と同様に難しい気がしました。したがって、アトムのようなロボットの子供に最初にやってもらう作業を想定したとき、最も困難そうなのは字や数字を決められた枠の中に書き込む作業、せんじ詰めれば運動制御だという結論になりました。
一方、人間の出現前、動物の脳は専ら運動制御に使われてきました。動物の脳は、運動制御のための機能を基本としているはずです。人間の脳は運動制御だけでなく、推論や論理演算など運動制御以外の機能を持っていますが、その回路は運動制御用の回路を原型として作られたに違いないと私は考えました。また、運動制御は物理的制限が多く、モデルに強い制約がかかるので、最初に取り組むには適切だと考えました。さらに、人間の運動制御に関しては、多くの実験がなされ、データが豊富に存在しています (Fitts 1954; Morasso 1981; Abend et al. 1982; Wolpert et al. 1994; Shadmehr and Mussa-Ivaldi 1994; Flanagan and Rao 1995; Harris and Wolpart 1998; Van der Geest and Frens 2002; Mazzoni and Krakauer 2006; Krakasuer et al. 2006; Pasalar et al. 2006; Yamamoto et al 2007; Diedrichsen 2007; Ostry et al.2010; Shadmehr and Krakauer 2008; Shadmehr et al. 2010; Izawa et al. 2008; Qian et al. 2013; Nashed et al. 2014)。得られているデータとの比較でモデルの検証が可能です。最後に、工学分野におけるロボットを含む自動機械の制御のために最適制御理論が発達してきました。そこで培われてきた数学体系を適用できる可能性があります。

Figure 3. キバナコスモスにとまるツマグロヒョウモンのオス。人間の出現以前、動物の脳は専ら運動制御に使われていたはず、、、。
4. 「計算論的神経科学」に出会う
そのように考えていた時に出会ったのが、「計算論的神経科学」という田中宏和氏の本でした (Tanaka 2019)。2021年の正月の三日間この本をざっと読み、運動制御理論と神経科学の間の広範な科学領域についての記述があることを知った私は、この本の内容を徹底的に理解することを志しました。そして、五十嵐潤さん、太田聡史さんの三人で輪講を始めたのは2022年の7月でした。それから2024年1月まで約1年半年間で13回の輪講を行い、件の本に書かれている式一つ一つに亘るまで徹底的な理解を目指しました。本の記述に疑義があるときは原著論文まで遡って糺しました。学生時代以来、久しぶりに徹底的な本読みでずいぶん頭の中が活性化しました。
そのような努力の中で、いくつか問題点が見えてきました。まず、運動制御の理論は、ラグランジュの未定係数法およびハミルトン形式を用いた最適問題解法の数学的枠組みを主に用いていました。これらは、私が学部生時代に大阪大学理科部物理学科で徹底的に叩きこまれた解析力学そのものでした。解析力学を用いる古典力学や量子力学は、エネルギーを時間積分した「作用」という量を最小化するという数学的形式を持っているのです(Goldstein et al. 2014; 保江2007 )。
次に、運動の最適制御理論が厳密な答えを与えるのは、問題が線形(状態方程式が定数の行列で記述され、評価関数が状態量の二次形式で与えられる)の場合に限られるということです。ところが実際に解析したい運動は非線形性が強い場合が多く、最適制御理論の適用がごく簡単(線形)な問題に限られていると田中氏を始めとした脳科学者が信じているらしいということでした。ところが、物理においては粒子の非線形な運動を「局所線形化」というテクニックを使って、たくさんの線形問題の積み上げによって厳密に求めるということを行います。この局所線形化のテクニックを人間やロボットの運動制御に用いれば、最適制御理論の適用範囲が大きく広がるに違いないとの印象を持ちました。
さらに、人間の脳の中にある外界もしくは運動器に関するモデル、いわゆる内部モデルについての議論に違和感を覚えました。著者の田中氏を始めとする脳・神経学者は、脳で順モデルが働いているのか逆モデルが働いているのかを議論しているようでした (Pasalar et al. 2006; Yamamoto et al 2007,Ostry et al.2010; Shadmehr and Krakauer 2008; Shadmehr et al. 201)。順モデルとは、力(トルク)を与えて運動器の各部分がどちらに向かって動くかを与えるモデルです。逆モデルは、その逆に、運動器の各部分がある時点でどこにあるべきかを設定して、それを実現する力(トルク)を与えるモデルです。前者は、いわゆる運動方程式を時間積分すればよいという意味で素直なので「順モデル」となり、後者はその逆なので「逆モデル」と言われるようになったようです。 しかし私は、「順モデルが成立していたら、逆モデルは成り立たない」とか、「脳のある場所で順モデルが成立していたら、逆モデルは脳の別の場所で成り立っているに違いない」というような二項対立的な画一的な考え方は、ちょっと違うかもしれないと思いました。
脳は同時にほぼ同じ場所で順逆両方のモデルを使って制御し、滑らかで効率的な運動制御を実現しているのではないかと私は考えていたのです。人間の眼からの情報は目標の大局的な位置を与えるので、逆モデル制御に向いています。一方で、体の内部情報(関節の角度や筋肉の出力、骨の軋み、三半規管からの姿勢の情報など)は順モデル制御に向いています。例えば、飛んでくるボールを手に持った棒で叩くことを考えましょう。このとき、眼からの大局的情報による逆モデル制御と肉体の内部情報による順モデル制御が複雑に絡み合なければ、このかなり難しい運動を実現できないだろうと私は考えました。あるよく設計された実験の結果、ある場合に順(もしくは逆)モデルが働いているという結果が得られている場合があります。しかしそのような場合でも、その裏で逆(もしくは順)モデルも同時に働いていることは十分あり得そうです。一方、現状で存在する実験結果から、その動作を否定することは困難なように私は思いました。 実際、最適制御理論では、必要な力は、その結果である各部の将来位置を考慮して「最適(評価関数を最小とする)」になるように対応する位置とともに同時に与えられるという意味で、「順」も「逆」もなく両者を一緒に解いていると考えるべきだと私は思っています。
5. 「最適制御神経回路理論」の構築へ
折から、最高速計算機の性能は2022年に1EFlopsを超えました(Figure 1)。つまり、計算能力の観点では、そろそろ技術的特異点が始まってもよいことになります。実際、最近の大規模言語モデルは人間のIQの平均値である100(人間の平均値)を超える性能を持ち始めています (Lott 2024)。これまで人間がやらざるを得なかった知的な労働を人工脳が代替することが可能になりつつあります。 大規模言語モデルの性能は、モデルに含まれるパラメータの数が多ければ多いほど良いといういわゆるスケール則が成り立っていることが話題になっています (Kaplan et al. 2020)。最新のモデルではパラメータ数が1兆個を超えつつあり、そのパラメータを決めるための学習に途方もない計算資源が使われています。人工知能の学習手法の効率化が、より大きな計算資源への投資とともに強く求められています。
一方で、前節に書いたような問題意識を持った私は、田中氏が記述した「計算論的神経科学」を全面的に再構築することを志し、この半年(現在は2024年9月)である程度の目途を得ました。それは、「最適制御神経回路理論」とでも名付けるべきもので、小行列の行列積と逆行列計算を多数回実行する形に定式化でき、神経細胞のみを用いての実現も不可能ではなさそうです。最適制御神経回路理論は人間の運動制御にとどまらず、深層学習や大規模言語モデルを含む人工神経回路網、すなわち人工知能一般の学習の効率化に対する数学的な枠組みを提供するものであることが分かってきました。つまり、人間の滑らかで効率的な身体操作を作り出すとともに、その回路を転用して推論や論理演算などを行う人間の脳の設計図への理解、さらには人間の脳を超えた人工知能実現への手がかりになりそうなのです。
このような状況の中で、脳と計算機と運動制御について俯瞰する科学エッセイシリーズを五十嵐さん、太田さんで手分けしてリレー形式で書いてみたら面白いかもしれないと考えました。田中氏の本の輪講の中でこの3人で様々な議論を長々としました。それは刺激に満ちたものでした。その知的興奮の一部でも読者に届けられればと考えています。このシリーズの中で戎崎は、新しい学問体系である「最適制御神経回路理論」の基礎論を展開してみようと思います。一方で、五十嵐さんは、脳のシミュレーションが専門、太田さんは人間の運動シミュレーションが専門ですので、それぞれの立場から人間の脳と人工知能を多角的に俯瞰する議論を展開していただけると考えています。
(初出:2025年3月14日、TEN (Tsunami, Earth, and Networking), 6, 14)
謝辞
まず、計算論的神経科学の著者、田中宏和氏に感謝します。この本は60代半ばの老科学者の消えようとする知的好奇心に再び火を灯し、新しい学問分野に挑戦するきっかけとなりました。また、この2年余りの間議論に付き合ってくれた五十嵐氏、太田氏に感謝したいと思います。
引用文献
1) Kurzweil, R. 2005, The Singularity Is Near, pp. 135–136. Penguin Group.
2) Yamazaki, T., Igarashi, J., Ebisuzaki, T., and Makino, J., 2017, Real-time simulation of a cat-scale artificial cerebellum on PEZY-SC processors, The Interna-tional Journal of High Performance Computing Ap-plications, 33, 155-168.
3) Igarashi, J., Yamaura, H., and Yamazaki, T. (2019). Large-Scale Simulation of a Layered Cortical Sheet of Spiking Network Model Using a Tile Partitioning Method. Front. Neuroinform. 13, 1–15. doi:10.3389/fninf.2019.00071.
4) Yamaura, H., Igarashi, J., and Yamazaki, T. (2020). Simulation of a Human-Scale Cerebellar Network Model on the K Computer. Front. Neuroinform. 14, 16. doi:10.3389/fninf.2020.00016.
5) Yamazaki, T., Igarashi, J., and Yamaura, H. (2021). Human-scale Brain Simulation via Supercomputer: A Case Study on the Cerebellum. Neuroscience 462, 235–246. doi:10.1016/J.NEUROSCIENCE.2021.01.014.
6) Igarashi, J., Yamazaki, T., Yamaura, H., Nomura, K., Sun, Z., Gutierrez, C. G., and Doya, K. (2022). K., A Spiking Neural Network Simulation of Layered Sheet of Cortico-Cerebello-Thalamic Circuit at Hu-man-Scale, Neuroscience 2023 Abstracts, 578.19
7) Fitts, P.M., 1954, The information capacity of the human motor system in controlling the amplitude of movement, Journal of Experimental Psychology, 47, 381-391. 8) Morasso, P., 1981, Spatial control of arm movements, Experimental Brain Research, 42, 223-227.
9) Abend, W., Bizzi, E. and Morraso, P., 1982, Human arm trajectory formation, Brain, 105, 331-348.
10) Wolpert, D.M., Ghahramani, Z., and Jordan, M.I., 1994, Perceptual distortion contributes to the curvature of human reaching movements, Experi-mental Brain Research, 98, 153-156.
11) Shadmehr, R. and Mussa-Ivaldi, F.A., 1994, Adaptive representation of dynamics during learn-ing of a motor task, Journal of Neuroscience, 14, 3208-3224.
12) Flanagan, J.R., and Rao, A.K., 1995, Trajec-tory adaptation to nonlinear visuomotor transfor-mation: evidence of motion planning in visually perceived space, Jpurnal of Neurophysiology, 74. 2124-2178.
13) Harris, C.M. and Wolpart, D.M., 1998, Sig-nal-dependent noise determines motor planning, Nature, 394, 780-784.
14) Van der Geest, J.N., and Frens, M.A., 2002, Recoding eye movements with video-oculography and scleral search coils: a direct comparison of two methods, Journal of Neuroscience Methods, 114, 185-195.
15) Mazzoni, P., and Krakauer, J.W., 2006, An implicit plan overrides an explicit strategy during visunomotor adaptation, Journal of Neuroscience, 26, 3642-3645.
16) Krakasuer, J.W., Mazzoni, P., Ghazizadeh, A., Ravindran, R., 2006, Generation of motor learning depends on the history prior action, PloS Biology, 4, e316.
17) Pasalar, S., Roitman, A.V., Durfee, W.K., Ebner, T.J., 2006, Force field effects on cerebellar Purkinje cell discharge with inmplications for internal trajectory, Scientific Reports, 5, 17659.
18) Yamamoto, K. Kawato, M., Kotosaka, S., Kitazawa, S., 2007, Encoding of movement dynam-ics by Prikinje cell sample spike activity during fast arm movements under resistive and assistive force fields, Journal of Neurophysiology, 97, 1588-1599.
19) Diedrichsen, J., 2007, Optimal Task-dependent change of bimanual feedback control and adapta-tion, Current Biplogy, 17, 1675-1679.
20) Ostry, D.J., Darainy, N., Mattar, A.A., Wing, J., and Gribble, P.L., 2010, Somatosensory plasticity and motor learning, Journal of Neuroscience, 26, 3642-3645.
21) Shadmehr, R. and Krakauer, J.W、2008A computational neuroanatomy for motor control, Experimental Brain Research, 185, 359-381. 22) Shadmehr, R., Smith, M.A., and Krakauer, J.W., 2010, Error correction, sensory prediction, and ad-aptation in motor control., Annual Review of Neu-roscience, 33, 89-108.
23) Izawa, J., Rane, T., Donchin O and Shadmehr, R., 2008, Motor Adaptation as a process of reopti-mization, Journal of Neutroscience, 28, 2883-2891.
24) Qian, N., Jiang, Y. Jiang, Z.P., Mazzoni, P., 2013, Movement duration, Fitts’s law and an infi-nite-horizon optimal feed-back control model for biological motor systems, Neural Computation, 25, 697-703.
25) Nashed、Y., Crevecoeur, F., and Scott, S.H., 2014, Rapid online selection between multiple mo-tor plans, Journal of Neuroscience, 34、1769‐1780.
26) 田中宏和、2019、計算論的神経科学 脳の運動制御・感覚処理機構の理論的理解へ、森北出版。
27) Goldstein, H., Poole, C.P. Jr., and Safko, J.L., 2014, Classical Mechanics, Pearson Educational Limited.
28) 保江邦夫、2007、量子力学と最適制御理論 確率量子化と確率変分学への誘い、海潮社
29) Lott, M. 2024, AIs ranked by IQ; AI passes 100 IQ for first time, with release of Claude-3, https://www.maximumtruth.org/p/ais-ranked-by-iq-ai-passes-100-iq 30) Kaplan, J., McCandlish, S., Henighan, T., Brown, T.B., Chess, B., Child, R., Gray, S., Radford, A., Wu, J., Amodei, D., 2020, Scaling Laws for Neural Language Models, https://arxiv.org/pdf/2001.08361.
初出 TEN (Tsunami, Earth, and Networking) 第6巻、pp14‐19 2025年3月14日
書籍版『科学はひとつ』のご案内
戎崎俊一 著
学而図書/四六判 並製320頁/本体2,400円+税
12年にわたり執筆されてきた記事を精選し、「地震と津波防災」など全9章に再編。すべての章に著者書き下ろしの解説を加えて集成した一冊。