練習問題2-5

式2-30を用いて\({\bf W}(t)\)を解析的に求めなさい。

練習問題2-5

状態空間モデルを定義する\(\bf A\)、\(\bf B\)、\(\bf R\)は、

\begin{equation} {\bf A}=\left( \begin{array}{ccc} 0&1&0\\ -\omega^2& 0&1\\ 0&0&0 \end{array}\right),\quad {\bf B}=\left( \begin{array}{c} 0\\ 0\\ 1 \end{array}\right),\quad {\bf R}=1 \tag{1} \label{eq1} \end{equation}

と与えられている。ここで、\(\omega =\sqrt{k_{\rm s}/m}\)は、系の固有振動数である。\(\bf A\)を対角化すると、

\begin{equation} {\bf P}=\left( \begin{array}{ccc} 1/\sqrt{2}ω&1/\sqrt{2}ω&1/\sqrt{2}ω\\ i/\sqrt{2}&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array}\right)\tag{2}\end{equation} \begin{equation}{\bf P}^{-1}=\left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2} ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2} ω\\ 0&0&\sqrt{2}/ω \end{array} \right)\tag{3}\end{equation} \begin{equation} {\bf Λ}=ω\left( \begin{array}{ccc} i&0&0\\ 0&-i&0\\ 0&0&0 \end{array} \right) \tag{4} \end{equation}

を得る。実際

\begin{eqnarray} {\bf P}{\bf P}^{-1}&=&\left( \begin{array}{ccc} 1/\sqrt{2}ω&1/\sqrt{2}ω&1/\sqrt{2}ω\\ i/\sqrt{2}&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array} \right)\left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2}ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2}ω\\ 0&0&\sqrt{2}/ω \end{array} \right)\\ &=&\left( \begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array} \right)\tag{5} \end{eqnarray} \begin{eqnarray} {\bf P}^{-1}{\bf P}&=&\left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2}ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2}ω\\ 0&0&\sqrt{2}/ω \end{array} \right)\left(\begin{array}{ccc} 1/\sqrt{2}/ω&1/\sqrt{2}/ω&1/\sqrt{2}/ω\\ i/\sqrt(2)&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array} \right)\\ &=&\left( \begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array} \right)\tag{6} \end{eqnarray}

\begin{eqnarray} {\bf PΛ{P}^{-1}}&=& \left( \begin{array}{ccc} 1/\sqrt{2}ω&1/\sqrt{2}ω&1/\sqrt{2}ω\\ i/\sqrt{2}&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array}\right) ω\left( \begin{array}{ccc} i&0&0\\ 0&-i&0\\ 0&0&0 \end{array} \right) {\bf P}^{-1} \\ &=&ω\left( \begin{array}{ccc} i/\sqrt{2}ω&-i/\sqrt{2}ω&0\\ -1/\sqrt{2}&-1/\sqrt{2}&0\\ 0&0&0 \end{array}\right) \left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2}ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2}ω\\ 0&0&\sqrt{2}/ω \end{array} \right) \\ &=&ω\left( \begin{array}{ccc} 0&1/ω&0\\ -ω&0&1/ω\\ 0&0&0 \end{array} \right)\\ &=&\left( \begin{array}{ccc} 0&1&0\\ – ω^2&0&1\\ 0&0&0 \end{array}\right)\\ &=&{\bf A} \tag{7} \end{eqnarray}

である。

\(\hat{t}=t-t_{\rm f}\)とおくと、式2-31より

\begin{eqnarray} &&{\bf V}(t)={\bf P}e^{-Λ(t-t_{\rm f})}{\bf P}^{-1}\\
&=&\left( \begin{array}{ccc} 1/\sqrt{2}ω&1/\sqrt{2}ω&1/\sqrt{2}ω\\ i/\sqrt{2}&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array}\right)
\left( \begin{array}{ccc} e^{-iω\hat{t}}&0&0\\ 0&e^{iω\hat{t}}&0\\ 0&0&1 \end{array}\right){\bf P}^{-1}\\ &=&\left( \begin{array}{ccc} e^{-iω\hat{t}}/\sqrt{2}ω&e^{iω\hat{t}}/\sqrt{2}ω&1/\sqrt{2}ω\\ ie^{-iω\hat{t}}/\sqrt{2}&-ie^{iω\hat{t}}/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array}\right)
\left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2}ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2}ω\\ 0&0&\sqrt{2}/ω \end{array} \right) \\ &=&\left( \begin{array}{ccc} e^{-iω\hat{t}}/2+e^{iω\hat{t}}/2&-ie^{-iω\hat{t}}/2ω+ie^{iω\hat{t}}/2ω&-e^{-iω\hat{t}}/2ω^2-e^{iω\hat{t}}/2ω^2+1/ω^2\\ iωe^{-iω\hat{t}}/2-iωe^{iω\hat{t}}/2&e^{-iω\hat{t}}/2+e^{iω\hat{t}}/2&-ie^{-iω\hat{t}}/2ω+ie^{iω\hat{t}}/2ω\\ 0&0&1 \end{array} \right) \\ &=&\left( \begin{array}{ccc} (e^{iω\hat{t}}+e^{-iω\hat{t}})/2&i(e^{iω\hat{t}}-e^{-iω\hat{t}})/2ω&-((e^{iω\hat{t}}+e^{-iω\hat{t}})/2-1)/ω^2\\ -iω(e^{iω\hat{t}}-e^{-iω\hat{t}})/2&(e^{iω\hat{t}}+e^{-iω\hat{t}} )/2ω&i(e^{iω\hat{t}}-e^{-iω\hat{t}} )/2ω\\ 0&0&1 \end{array} \right) \\ &=&\left( \begin{array}{ccc} \cos(ω\hat{t})&-\sin(ω\hat{t})/ω&-(\cos(ω\hat{t})-1)/ω^2\\ ω\sin(ω\hat{t})&\cos(ω\hat{t})&-\sin(ω\hat{t})/ω\\ 0&0&1 \end{array} \right) \tag{8} \end{eqnarray}

を得る。また、

\begin{eqnarray} {\bf U}(t)&=&{\bf V}(t)^{\rm T}\\ &=&\left( \begin{array}{ccc} \cos(ω\hat{t})&-\sin(ω\hat{t})/ω&-(\cos(ω\hat{t})-1)/ω^2\\ ω\sin(ω\hat{t})&\cos(ω\hat{t})&-\sin(ω\hat{t})/ω\\ 0&0&1 \end{array} \right)^{\rm T}\\ &=&\left( \begin{array} ω\cos(ω\hat{t})&ω\sin(ω\hat{t})&0\\ -\sin(ω\hat{t})/ω&\cos(ω\hat{t})&0\\ -(\cos(ω\hat{t})-1)/ω^2&-\sin(ω\hat{t})/ω&1 \end{array} \right) \tag{9} \end{eqnarray} である。また、式\ref{eq1}より、 \begin{eqnarray} {\bf BR}^{-1} {\bf B}^{\rm T}&=&\left( \begin{array}{c} 0\\0\\1 \end{array} \right) 1^{-1} \left( \begin{array}{ccc} 0&0&1 \end{array} \right) &=&\left( \begin{array}{ccc} 0&0&0\\ 0&0&0\\0&0&1 \end{array} \right) \tag{10} \end{eqnarray}

さらに、

\begin{eqnarray} {\bf {P}^{-1} BR}^{-1} {\bf B}^{\rm T} {{\bf P}^{-1}}^{\rm T}&=&\left( \begin{array}{ccc} ω/\sqrt{2}&-i/\sqrt{2}&-1/\sqrt{2}ω\\ ω/\sqrt{2}&i/\sqrt{2}&-1/\sqrt{2}ω\\ 0&0&\sqrt{2}/ω \end{array} \right) \left( \begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&1 \end{array} \right) {{\bf P}^{-1}}^{\rm T} \\ &=&\left( \begin{array}{ccc} 0&0&1/(\sqrt{2} ω)\\ 0&0&1/(\sqrt{2} ω)\\ 0&0&\sqrt{2}/ω) \end{array} \right)\left( \begin{array}{ccc} ω/\sqrt{2}&ω/\sqrt{2}&0\\ -i/\sqrt{2}&i/\sqrt{2}&0\\ -1/\sqrt{2} ω&-1/\sqrt{2} ω&\sqrt{2}/ω \end{array} \right)\\ &=& \frac{1}{ω^2} \left( \begin{array}{ccc} 1/2&1/2&-1\\ 1/2&1/2&-1\\ -1&-1&2 \end{array} \right)\\ &=&\left( \begin{array}{ccc} 1/2ω^2&1/2ω^2&-1/ω^2\\ 1/2ω^2&1/2ω^2&-1/ω^2\\ -1/ω^2&-1/ω^2&2/ω^2 \end{array} \right) \tag{11} \end{eqnarray}

を得る。さらに、

\begin{eqnarray} &&e^{-{\bf Λ}(t_1-t_{\rm f} ) } {\bf P ̃BR}^{-1} {\bf B}^{\rm T} {{\bf P}^{-1}}^{\rm T} e^{-{\bf Λ}(t_1-t_{\rm f}) }\\ &=&\frac{1}{ω^2} \left( \begin{array}{ccc} e^{-iω\hat{t}}&0&0\\ 0&e^{iω\hat{t}}&0\\ 0&0&1 \end{array} \right)\left( \begin{array}{ccc} 1/2&1/2&-1\\ 1/2&1/2&-1\\ -1&-1&2 \end{array} \right)\left( \begin{array} ee^{-iω\hat{t}}&0&0\\ 0&e^{iω\hat{t}}&0\\ 0&0&1 \end{array} \right)\\ &=&\frac{1}{ω^2} \left( \begin{array}{ccc} e^{-iω\hat{t}}/2&e^{-iω\hat{t}}/2&-e^{-iω\hat{t}}\\ e^{iω\hat{t}}/2&e^{iω\hat{t}}/2&-e^{iω\hat{t}}\\ -1&-1&2 \end{array} \right)\left( \begin{array}{ccc} e^{-iω\hat{t}}&0&0\\ 0&e^{iω\hat{t}}&0\\ 0&0&1 \end{array} \right) \\ &=&\frac{1}{ω^2} \left( \begin{array}{ccc} e^{-i2ω\hat{t}}/2&1/2&-e^{-iω\hat{t}}\\ 1/2&e^{i2ω\hat{t}}/2&-e^{iω\hat{t}}\\ -e^{-iω\hat{t}}&-e^{iω\hat{t}}&2 \end{array} \right) \\
&=&\left( \begin{array}{ccc} e^{-i2ω\hat{t}}/2ω^2&1/2ω^2&-e^{-iω\hat{t}}/ω^2\\ 1/2ω^2&e^{i2ω\hat{t}}/2ω^2&-e^{iω\hat{t}}/ω^2\\ -e^{-iω\hat{t}}/ω^2&-e^{iω\hat{t}}/ω^2&2/ ω^2\end{array} \right) \tag{12} \end{eqnarray}

となる。その上、

\begin{eqnarray} &&\int_{t_{\rm f}}^te^{-{\bf Λ}(t_1-t_{\rm f})} {\bf P}^{-1}{\bf BR}^{-1} {\bf B}^{\rm T} {{\bf P}^{-1}}^{\rm T} e^{-{\bf Λ}(t_1-t_{\rm f})} dt_1 \\ &=&\int_{t_{\rm f}}^t\left( \begin{array}{ccc} e^{-i2ω(t_1-t_{\rm f})}/2ω^2&1/(2ω^2)&-e^{-iω(t_1-t_{\rm f})}/ω^2\\ 1/(2ω^2)&e^{i2ω(t_1-t_{\rm f})}/(2ω^2)&-e^{iω(t_1-t_{\rm f})}/ω^2\\ -e^{-iω(t_1-t_{\rm f})}/ω^2&-e^{iω(t_1-t_{\rm f})}/ω^2&2/ω^2 \end{array} \right) dt_1 \\ &=&\left[ \left( \begin{array}{ccc} -e^{-2iω(t_1-t_{\rm f})}/(4iω^3)&t_1/(2ω^2)&e^{-iω(t_1-t_{\rm f})}/(iω^3)\\ t_1/(2ω^2)&e^{2iω(t_1-t_{\rm f})}/(4iω^3)&-e^{iω(t-t_{\rm f})}/(iω^3)\\ e^{-iω(t_1-t_f)}/(iω^3)&-e^{iω(t_1-t_{\rm f})}/(iω^3)&2t_1/ω^2 \end{array} \right)\right]^t_{t_{\rm f}}\\ &=&\frac{1}{ω^3} \left( \begin{array}{ccc} i(e^{-2iω\tilde{t}}-1)/4&ω\tilde{t}/2&-i(e^{-iω\tilde{t}}-1)\\ ω\tilde{t}/2&-i(e^{2iω\tilde{t}}-1)/4&i(e^{iω\tilde{t}}-1)\\ -i(e^{-iω\tilde{t}}-1)&i(e^{iω\tilde{t}}-1)&2ω\tilde{t} \end{array}\right) \tag{13} \end{eqnarray}

を得る。式11より、

\begin{eqnarray} &&{\bf W}(t)\\ &=&{\bf P}(\int_t^{t_{\rm f}} e^{-{\bf Λ}(t_1-t_{\bf f})} {\bf P}^{-1} {\bf BR}^{-1} {\bf B}^{\rm T} {{\bf P}^{\rm T}}^{-1} e^{-{\bf Λ}(t_1-t_{\rm f})} dt_1) {\bf P}^{\rm T} \\ &=& \left( \begin{array}{ccc} 1/\sqrt{2}ω&1/\sqrt{2}ω&1/\sqrt{2}ω\\ i/\sqrt{2}&-i/\sqrt{2}&0\\ 0&0&ω/\sqrt{2} \end{array}\right)\\ &\times&\frac{1}{ω^3}\left( \begin{array}{ccc} i(e^{-2iω\tilde{t}}-1)/4&ω\tilde{t}/2&-i(e^{-iω\tilde{t}}-1)\\ ω\tilde{t}/2&-i(e^{2iω\tilde{t}}-1)/4&i(e^{iω\tilde{t}}-1)\\ -i(e^{-iω\tilde{t}}-1)&i(e^{iω\tilde{t}}-1)&2ω\tilde{t} \end{array}\right){\bf P}^{\rm T}\\ &=&\frac{1}{ω^3} \left( \begin{array}{c} i(e^{-2iω\hat{t}}-1)/4\sqrt{2}ω+\hat{t}/2\sqrt{2}-i(e^{-iω\hat{t}}-1)/\sqrt{2}ω\\ -(e^{-2iω\hat{t}}-1)/4\sqrt{2}ω+iω\hat{t}/2\sqrt{2}\\ -i(e^{-iω\hat{t}}-1)ω/\sqrt{2} \end{array} \right. \end{eqnarray} \begin{eqnarray} &&\left. \begin{array}{cc} \hat{t}/2\sqrt{2}-i(e^{2iω\hat{t}}-1)/4\sqrt{2}i+i(e^{iω\hat{t}}-1)/\sqrt{2}ω&-i(e^{iω\hat{t}}-1)/\sqrt{2}ω+i(e^{iω\hat{t}}-1)/\sqrt{2}ω+\sqrt{2}\hat{t}\\ iω\hat{t}/2\sqrt{2}-(e^{2iω\hat{t}}-1)/4\sqrt{2}&(e^{-iω\hat{t}}-1)/\sqrt{2}+(e^{iω\hat{t}}-1)/\sqrt{2}\\ i(e^{iω\hat{t}}-1)ω/\sqrt{2}&\sqrt{2}ω^2\hat{t} \end{array} \right)\\ &\times&\left( \begin{array}{ccc} 1/\sqrt{2}ω&i/\sqrt{2}&0\\ 1/\sqrt{2}ω&-i/\sqrt{2}&0\\ 1/\sqrt{2}ω&0&ω/\sqrt{2} \end{array} \right) \end{eqnarray}\begin{equation} =\frac{1}{ω^3} \left( \begin{array}{c} 3ω\hat{t}/2-i(e^{2iω\hat{t}}-e^{-2i(ω\hat{t}})/8ω^2+i(e^{iω\hat{t}}-e^{-iω\hat{t}})/ω^2\\ -(e^{2iω\hat{t}}+e^{-2iω\hat{t}}-2)/8ω+(e^{iω\hat{t}}+e^{-iω\hat{t}}-2)/2ω\\ i(e^{iω\hat{t}}-e^{-iω\hat{t}} )/2+ω\hat{t} \end{array} \right.\\ \left. \begin{array}{c} -(e^{2iω\hat{t}}+e^{-2iω\hat{t}}-2)/8ω+(e^{iω\hat{t}}+e^{-iω\hat{t}}-2)/2ω\\ i(e^{2iω\hat{t}}-e^{-2iω\hat{t}} )/8+ω\hat{t}/2\\ (e^{iω\hat{t}}+e^{-iω\hat{t}}-2)ω/2 \end{array} \\ \begin{array}{c} i(e^{iω\hat{t}}-e^{-iω\hat{t}} )/2+ω\hat{t} \\ (e^{iω\hat{t}}+e^{-iω\hat{t}}-2)ω/2\\ ω^2\hat{t} \end{array} \right)\end{equation}  \begin{equation}=\frac{1}{ω^3} \left( \begin{array}{c} (3ω\hat{t}/2+\sin(2ω\hat{t})/4-2\sin(ω\hat{t}))/ω^2 \\ -(\cos(2ω\hat{t})-1)/4ω+(\cos(ω\hat{t})-1)/ω\\ -\sin(ω\hat{t})+ω\hat{t} \end{array}\right. \\ \left. \begin{array}{cc} -(\cos(2ω\hat{t})-1)/4ω+(\cos(ω\hat{t})-1)/ω&-\sin(ω\hat{t})+ω\hat{t} \\-\sin(2ω\hat{t})/4+ω\hat{t}/2&(\cos(ω\hat{t})-1)ω\\ (\cos(ω\hat{t})-1)ω&ω^2\hat{t} \end{array} \right) \tag{14} \end{equation}

\(ω=1\,{\rm rad\, s}^{-1}\)の場合の数値解と解析解をFigure 1で示す。両者はよく一致している。

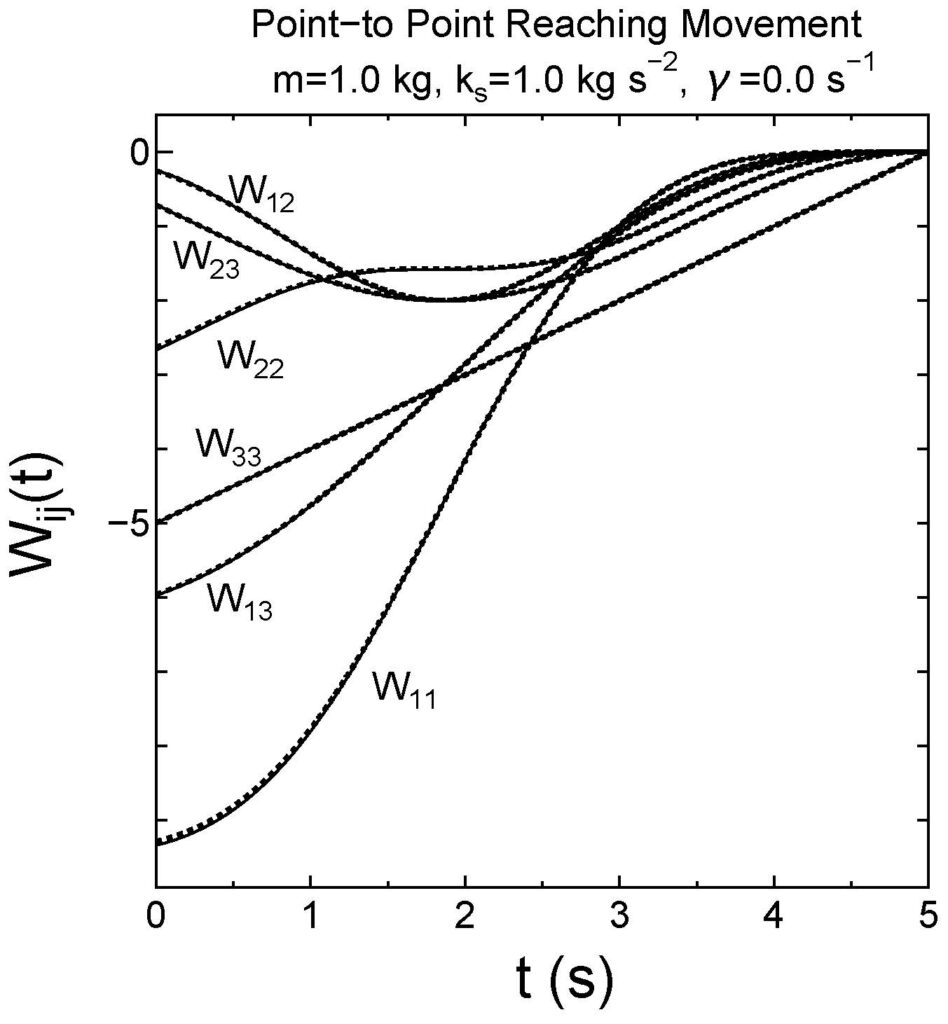
Figure 1 行列\({\bf W}(t)\)の独立成分の時間変化。\(ω=1\, {\rm rad\, s}^{-1}\)の場合。数値解（実線）と解析解（点線）はよく一致している。

書籍版『科学はひとつ』のご案内

科学はひとつ　宇宙物理学者による知的挑戦の記録
戎崎俊一 著
学而図書／四六判 並製320頁／本体2,400円＋税

12年にわたり執筆されてきた記事を精選し、「地震と津波防災」など全9章に再編。すべての章に著者書き下ろしの解説を加えて集成した一冊。

書誌情報はこちらから