地震発生の断層弁(水圧破砕)モデル
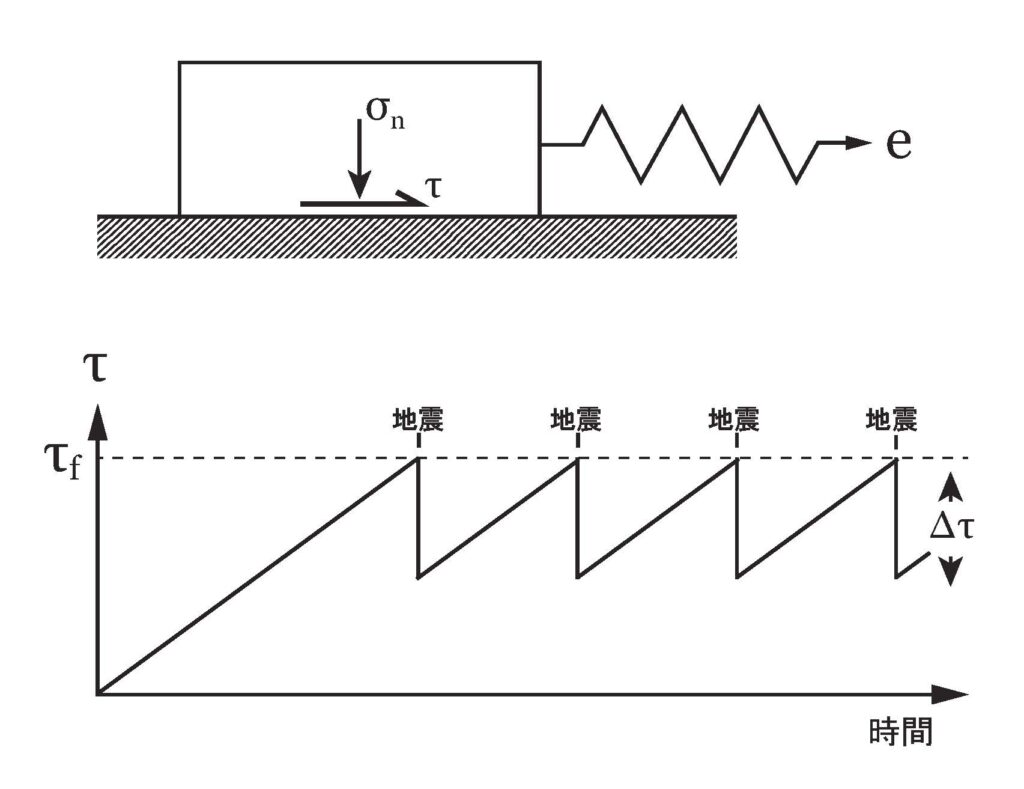
Figure 1 地震発生のアスペリティ(固着)モデル(Sibson 1993を元に作成)
地震の発生は、多くの場合物体の固着・滑り運動(stick-slip motion)で説明されています。例えばこんな感じです。水平な面の上に物体が載っており、バネを通して引っ張られています(Figure 1)。バネが伸びるにつれて床との間の応力\(\tau\)が増加し、耐応力限界\(\tau_{\rm f}\)を超えると物体が動き始めます。その条件は、
\(\hspace{5mm} \tau \gt \tau_{\rm f} \tag{1} \)
で与えられます。しばらく動いてバネが縮むと、物体に働く力が減って再び静止します。このような固着と滑りを繰り返す振動的な固着・滑り運動が繰り返されます。
同様の現象が地殻を構成する岩盤内の断層でも起きると考えられています。断層の耐応力限界\(\tau_{\rm f}\)は、断層面に対して垂直に働く垂直応力\(\sigma_{\rm n}\)に比例します。この耐応力限界が滑り摩擦力より大きいので振動的な固着・滑り運動が発生します。その滑りが地震に対応すると説明されてきました。これがいわゆるアスペリティ(固着)モデルで、地震発生の最も有力なモデルとされています。
しかし、実際には岩盤内の断層には流体(ミネラルを含んだ高温の水:いわゆる温泉水)が存在していることがあります。断層の耐応力限界\(\tau_{\rm f}\)は、垂直応力\(\sigma_{\rm n}\)と流体圧力\(p_{\rm f}\)、そして固着力\(C\)を使って
\(\hspace{5mm}\tau_{\rm f} = C+\mu_{\rm f} (\sigma_{\rm n} – p_{\rm f}) \tag{2} \label{eq2}\)
と表されます。ここで、\(\mu_{\rm f}\)は断層の静止摩擦係数です。断層の滑り方向には固着力が弱いので式\ref{eq2}の第一項は第二項に比べて無視できます。つまり、
\(\hspace{5mm}\tau_{\rm f} =\mu_{\rm f} (\sigma_{\rm n} – p_{\rm f}) \tag{3}\)
と書けます。ここで重要なことは、\(p_{\rm f}\)が大きくなって\(\sigma_{\rm n}\)に近くなると\(\tau_{\rm f}\)が小さくなってしまうことことです。したがって、応力\(\tau\)が全く変わらなくても、何らかの理由で断層内に水が溜まって流体圧力\(p_{\rm f}\)が上がることで、耐応力\(\tau_{\rm f}\)が小さくなり、\(\tau \gt \tau_{\rm f}\)となりすべり面に圧がかからなくなって、断層の滑り、すなわち地震が発生します(Figure 2)。このような機構による破壊現象は水圧破砕と呼ばれています。また、Figure 3のように、流体圧力とともに応力も変化する場合もあり得ます。
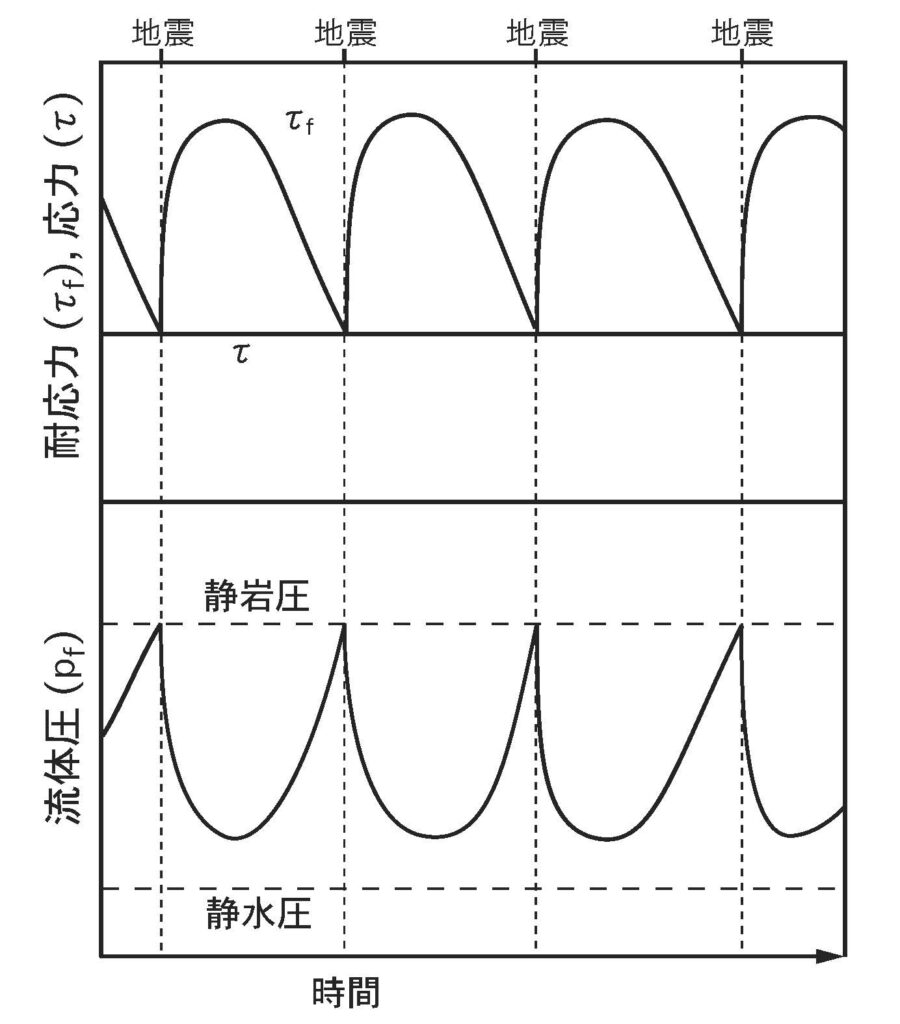
Figure 2 流体圧の上昇による断層滑り(地震の発生)。流体圧が上昇する結果、τ>τ_fとなって断層滑り(地震)が発生する。
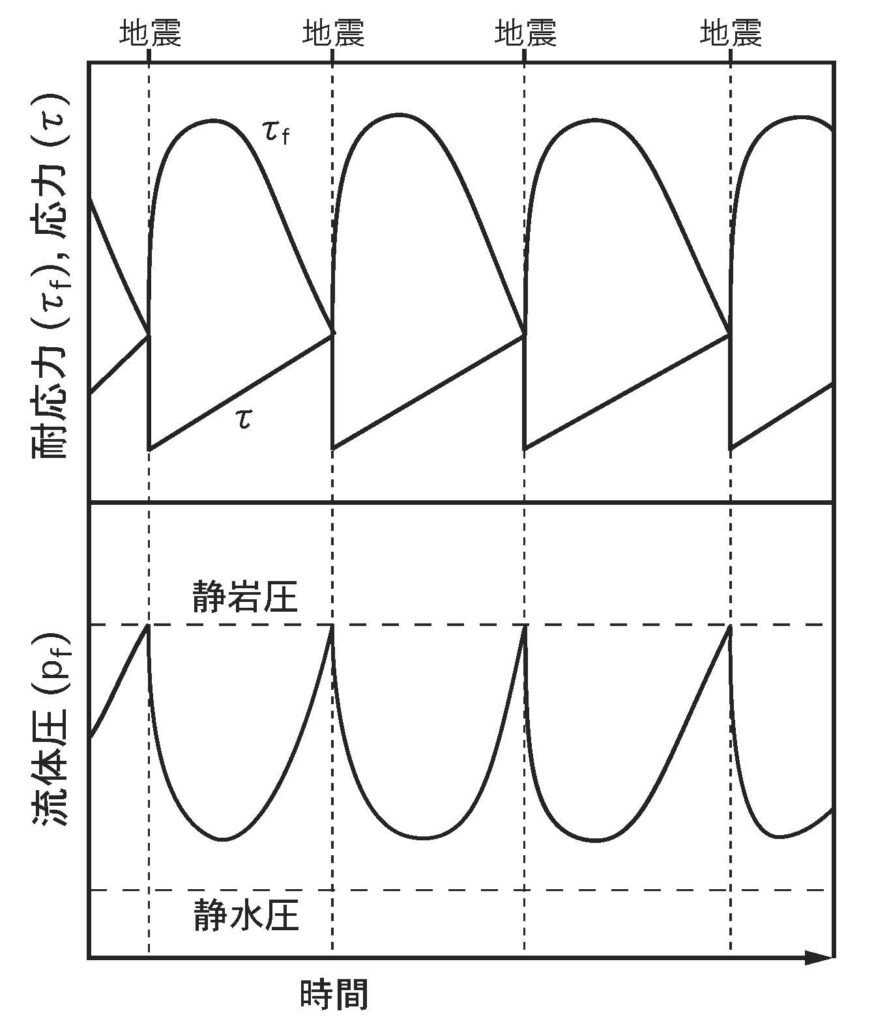
Figure 3 流体圧とともに応力も変化する場合。
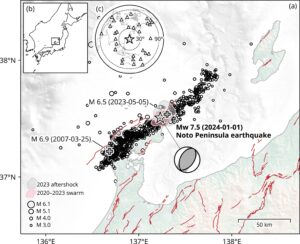
Sibson (1992)は、この水圧破砕により地震が発生すると指摘しました。垂直に近いすべり面を持った断層があったとしましょう(Figure 4)。その半ばに不透水層があってその下から流体(上記の温泉水)が定常的に供給されている状況を考えましょう。地震前は、断層も水を通さないので、その下に大量の流体が溜まり流体圧力\(p_{\rm f}\)が上昇します。そして、それが断層の垂直応力\(\sigma_{\rm n}\)(多くの場合は、その上に載っている岩盤を支えるために必要な圧力:静岩圧)を超えると圧力破砕が発生して断層が滑ります。そのとき断層内の不透水層が破壊され、溜まった流体が地上に噴出します。温泉水は多くのシリカを含んでいます。表層近くの低温部分でそれが析出し、流路が再び閉じてしまいます。そして、シリカが析出してできた水晶(シリカ)の岩脈が後に残ります。このように断層が地震のたびに開閉する弁として働く断層弁モデルで地震発生を説明することができます。
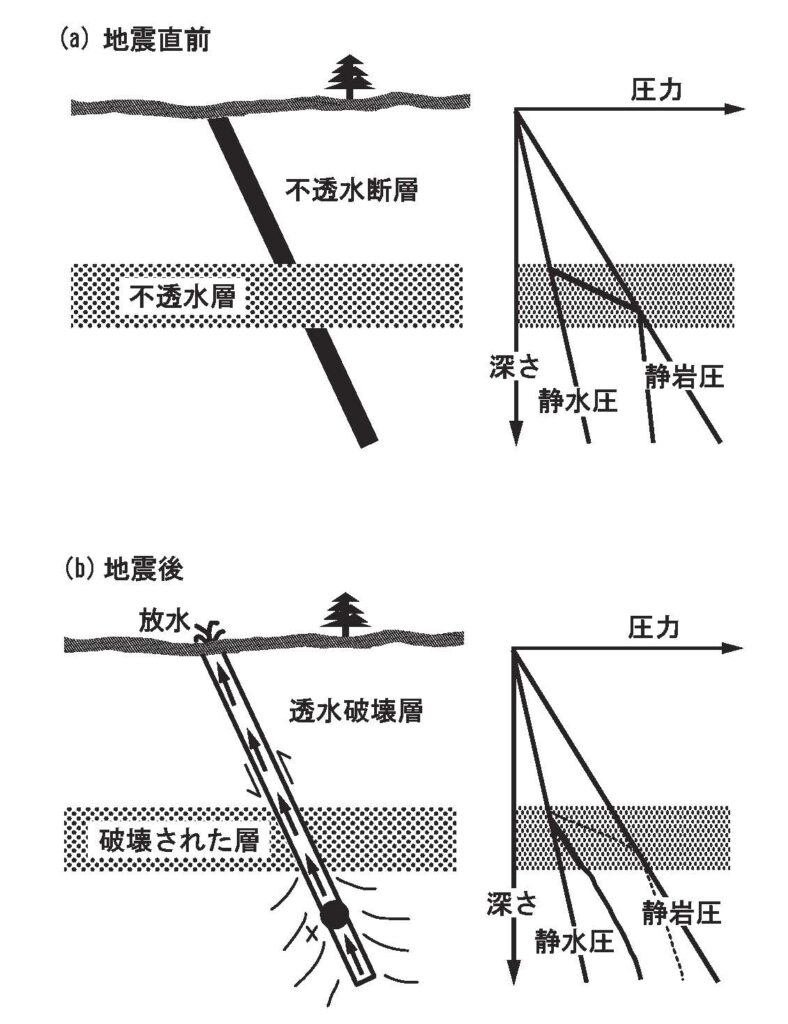
Figure 4 地震発生の断層弁(水圧破砕)モデル(Sibson 1993を元に作成)
プレート沈み込み帯においても、大量の水を含んだプレートの岩石がその沈み込みによる温度と圧力の上昇の結果、相変化を起こして水を追い出して流体を生じさせることが分かっています。このような機構で必然的に発生した流体が、プレート境界付近に蓄積して流体圧力が上昇し、圧力破砕をおこして巨大地震のきっかけになる可能性が指摘されています(大坪2022)。この断層弁(水圧破砕)モデルが正しい場合、アスペリティ(固着)モデルを用いて構築されてきたこれまでの地震予知の議論は、根本的な変更が必要になります。
また、火山噴火は、断層弁からの流体噴出の最も活発な場合と位置付けることもできるかもしれません。火山から噴出するマグマは大量の水を含んでいます。岩石は水を含むと大幅に融点が下がって融けてマグマとなるのです。マグマは温泉水の中でシリカが多い(むしろシリカの方が多い)場合に相当すると考えるべきでしょう。地殻内で起きた水圧破砕イベントの中で、流体(マグマ)が地表まで届いて激しく噴出した場合が火山噴火、流体の移動の大部分が地下で終わったものが地震と考えるべきかもしれません[1]。
ここで大事なことは、火山噴火については山体の膨張を監視することで予知が可能かもしれないということです。とすれば、地殻深部(深さ5-10km)における流体の動きを監視すれば、地震予知も原理的には可能であるということになります。また、その深度までボーリングして流体(温泉水)を抜き、流体圧を下げることができれば、地震発生を食い止めることができるかもしれません。その結果得られる高温の流体を用いての地熱発電も考えられます。それを実現するとすれば、5km以上の高深度ボーリングにかかる膨大な費用捻出の問題と高温流体からのシリカの析出によるパイプ封止の問題を克服しなければなりません。
[1] 火山噴火と地震は似た現象であり、岩石中に走る水晶(シリカ)の岩脈が地震の化石であると筆者に教えたのは丸山茂徳先生でした。
1) Sibson, R.H., 1993, Implication of Fault-valve behaviour for rupture nucleation and recurrence, Tectonophysics, 211, 283-293.
2) 大坪誠、2022、巨大地震を発生後の亀裂形成による排水は地震が起こるための水圧に影響を与えるか?、GSJ地質ニュース、11、3-7 。
書籍版『科学はひとつ』のご案内
戎崎俊一 著
学而図書/四六判 並製320頁/本体2,400円+税
12年にわたり執筆されてきた記事を精選し、「地震と津波防災」など全9章に再編。すべての章に著者書き下ろしの解説を加えて集成した一冊。